The Number Line in the Common Core

Background

Fraction Web

The web of fraction knowledge has many strands, including unit fractions, general fractions, proper and improper fractions and mixed numbers, equivalence or renaming, comparison, addition and subtraction, multiplication and division. These strands get all mixed together in teaching. Students need to learn the different interpretations so they have deep enduring understanding. Using concrete objects that students are familiar with will help them to learn the skills and feel confident in knowing fractions.

The web of fractions has structures (numerator and the denominator), have types of fractions (proper, improper, and mixed), use the operations, and the relationships of the fractions (fraction to fraction, fraction to decimals, fraction to percent, and equivalent). Along with the fraction components, students need to know how to use the different models to demonstrate fraction in representation. Visual diagrams, geometric shapes, and objects are used to exhibit the area model, the set model, and the linear measurement techniques.

Methods of Representing Fractions

It is recommended to use rectangles, squares, and triangles to depict fractions because Navajo looms and rugs correlate with these examples. Creating a visual representation of a fraction with a rectangle subdivided into the appropriate number of equal sections as the denominator, and with the number of shaded sections equal to the numerator is the area model representation.

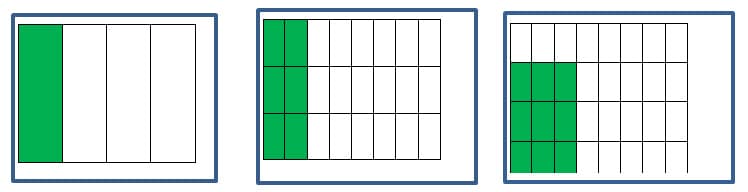
The full first column of the first figure represents ¼. The second figure has 8 equal columns, and 2 of them are shaded, so it represents 2/8; also the columns are divided in three pieces, making 24 equal small rectangles, of which 6 are shaded, so the figure illustrates that 2/8 = 6/24. In the third figure, the shaded region is 9/32 of the whole. The shaded area can also be thought of as ¾ of the columns it occupies, and these columns are 3/8 of the whole rectangle, so the picture can be taken as illustrating the multiplication ¾ x 3/8 = 9/32.

The set model is a display of individual shapes, with a distinguished subset to match the fraction. Below, are weaving tools as a set model. There are 6 tools for weaving. The 2 spindles are 2/6 of the whole collection, and the weaving comb is 1/6 of the collection.

Usually manipulatives, diagrams of pictures, and real objects are used to show understanding. Set models have numerous uses, including comparing like and unlike fractions, adding, subtracting, equivalent fractions, simplifying fractions, and more. Using weaving tools for the loom to demonstrate objects will help students visualize the patterns of fractions. These tools include weaving combs, baton, and sieve, skeins of wool of different colors, patterns of different rugs, and others. Students are able to sketch and orally explain, then write the set model created. 

In teaching fractions, it is important to have students become mindful of the quantity that represents the whole, or unit. A fraction, or any number, expresses the size of a quantity in relation to a unit. In the area model, the unit is usually understood to be the whole rectangle. In a set model, the unit is usually understood to be the whole set. But in some situations, the unit may be chosen differently. It is essential to have students always specify the unit to which a fraction refers, until it becomes an automatic process.¹

The linear measurement model is a concrete version of the number line method. Linear measurement plays an important role in creating a Navajo loom and rug. The number line is created to indicate numbered markings as unit segments on a line. For example the distance from 0 to 1 is known as a unit segment and additional units of whole numbers are marked at the same distance, consecutively. My students will create a loom from a piece of cardboard that has lines marked consecutively by short cuts, horizontally at the bottom of the cardboard. The distance between these short cuts is the warp width which is the anchor for the string. The stripe patterns created vertically are the fractional parts of the whole rug, known as the weft. These fraction components are also marked along a line resembling a number line.

The warp is cut into sections of ⅛ of an inch marked horizontally on each end of the cardboard. These marks will correspond to the unit segments on a number line. The warp cuts are for the threads stretched lengthwise. The wefts are the strings woven between and through the warp strands. The weft determines the vertical patterns of the striped rug and will establish the fraction part to a whole.

The Number Line

The number line can be thought of as an ideal ruler. It is a natural tool to use in weaving, or in any activity involving length measurement. Other tools for length measurement, especially for showing fractions of a unit length, are fraction strips and fraction bars. Cuisenaire rods can also be used to teach about length, especially the addition of lengths. When using the number line, it is not necessary to show the whole line, and in particular, the zero or origin does not need to be displayed. However, it is important for students to understand the Measurement Principle:

The number that labels a point on the number line tells the distance of the point from the origin, as a multiple of the unit length.

The distance between any two points labeled by consecutive whole numbers is always equal to the unit length.²

The features of a line are the order, distance, and length. These features are used to introduce a unit length/bar, and compare other lengths to multiples of the unit.³ To form a number line, first choose an origin (“0”), then choose a unit interval, (the other end from 0 is “1”), and lay off unit intervals moving to the right (i.e. + direction).⁴ Once a unit segment has been chosen on a given straight line, the places of all the whole numbers are fixed on the line. ⁵   In fact, all numbers are assigned to points. However, it is takes more work to determine where other numbers should go.