From Arithmetic to Algebra: Variables, Word Problems, Fractions and the Rules

Geometric (Exponential) Sequences

A geometric sequence is characterized by the common (constant) ratio, r. Each term is found by multiplying the previous term by the common ratio. The structure of the explicit equation of a geometric sequence can be analyzed using a table in a way similar to the first difference table for arithmetic sequences. To start analyzing a sequence, the ratio between two consecutive terms is calculated using the definition r_n=a_n+1/a_n, and then checking to see if the ratios are constant. Only if the ratios are constant, do we have a geometric sequence. In my classes, I plan to have students try analyzing examples that are geometric sequences while we study linear sequences to see what observations and conjectures they make. I would then show them how to find the ratio between consecutive terms and build an equation as outlined in the following exercise.

Exercise: Consider the sequence 3,6,12,24,48,…. Determine if the sequence is arithmetic, geometric or neither.

We begin by analyzing the sequence. We can observe that the sequence is not arithmetic because the difference between two consecutive terms is not constant. For example, ∆₁=6-3=3, but  ∆₂=12-6=6. Also ∆₃=24-12=12. The differences seem to be getting bigger and bigger. At any rate, they are certainly not constant.

To check if the sequence might be geometric, we compute the ratio between two consecutive terms to find r₁, r₂, r₃, and r₄. The key fact that I would point out to my students is that the ratio is the same value, and that this feature implies that the sequence is indeed geometric.

Since the ratio is constant, the sequence is geometric. To build an explicit equation, we can set up a ratio table for the geometric sequence that is analogous to the difference table used to analyze the arithmetic sequence.

Using a procedure similar to arithmetic sequences, each term can be written as the product of the first term and some number of copies of the constant ratio, That is, a_n is a product of a₁ and a power of the common ratio r.

a₁=3

a₂=3∙2

a₃=3∙2∙2

a₄=3∙2∙2∙2

a₅=3∙2∙2∙2∙2

…

At this step, I would ask my students to count the number of times we multiply the first term, 3, by the common ratio, 2. I would then show that we can rewrite each term as a product of a₁ with some power of the common ratio, by using the product property of exponents with the common ratio as the base. This would also be an opportunity to discussing with your students that the product property of exponents is a consequence of (a generalized version of) the Associative Rule for multiplication. I would then ask my students to, conjecture about the number of times we multiply by the common ratio to obtain the a_n term. Once we know this quantity, we can write the explicit equation.

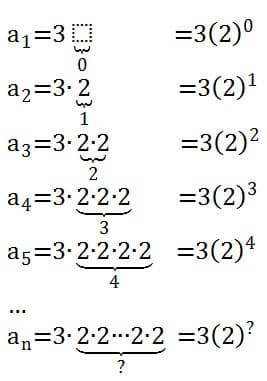
For any term in the sequence, notice the exponent of the common ratio is one less than the term number. This connection between the term number and the exponent of the common ratio can be made more obvious by rewriting the exponents asthe term number, minus 1. Note that this process parallels the structure for arithmetic sequences.

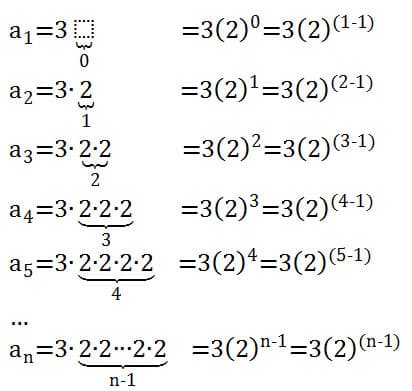
Extending the observations for the first five terms in the sequence, we can generalize the results to the nth term gives us the equation a_n=3(2)^n-1 representing our geometric sequence. After this example, I may have some students work with another geometric sequence with the goal of writing an equation. I anticipate some students will be ready to work independently, while smaller groups of students would work with either myself or my co-teacher as we go through additional examples.

The General Geometric Sequence

The structure of the process showing how to find an algebraic representation for geometric sequences follows a structure similar to the method for finding an arithmetic equation. The variable choice in the exercise is purposely meant to lead to the equation, a_n=a₁(r)^(n-1), which is found in the Big Ideas Integrated curriculum, as well as other math textbooks. I would demonstrate this example to my students to show where the formula in their textbook comes from.

Exercise: Suppose we know a sequence is geometric with first term a₁ and a constant ratio r. Can we find a formula for a_n?

In my classes, I would use the example in the section above, and point out that we can replace the 3 with a₁ and the 2 with r. I would make sure to point out that we are able to write the equation because there is a constant ratio. This would give us the following: 

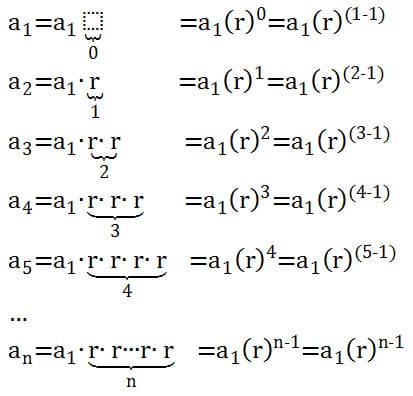
From this procedure, we have a_n=a₁(r)^n-1.

This is the same formula, which is the definition of a geometric sequence, found in the Larson textbook used by my students.

Recursive Equations for Geometric Sequences

We can use the structure to write the recursive form of a geometric sequence. This recursive formula follows directly from the definition of successive ratio and the condition that it be a fixed number r, if the sequence is geometric, i.e., the definition of geometric sequence. The main job here is to get students to understand that this is an immediate consequence of the definitions.

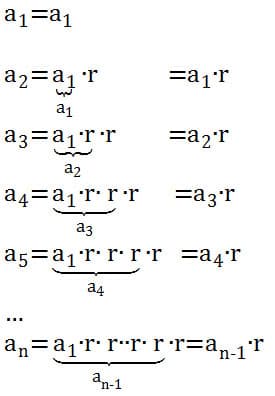
From this procedure, we have a recursive form with first term a₁ and nth term a_n=a_n-1∙r.