From Arithmetic to Algebra: Variables, Word Problems, Fractions and the Rules

Additional Problems

The following are example problems that can be modeled by each of the special cases of problems, or other types of sequences.

Arithmetic/Linear

1. A bridge railing is to be formed by placing equilateral triangles in a row. Starting with the first triangle, each subsequent triangle is placed so that it shares one side with the triangle before it. It takes three rods to build the first triangle, 5 rods to build two triangles, and 7 rods to build three triangles. The contractor wants to find the number of rods represented by t_n, the nth term of the sequence {3,5,7,…, t_n}.

2. Some types of bamboo plants can grow 4cm every hour. If one of these bamboo plants is 18cm tall, write an expression for the height (in cm) of the bamboo after h hours?

3. A decorative railing is to be constructed from sections in the shape of a regular hexagon placed such that two hexagons share 1 side. Create a sequence for t₁ to t₁₀ representing the number of metal rods needed to build from one to ten sections. Write a rule for t_n, the number of metal rods needed to build n sections of railing.

Geometric/Exponential

4. A rubber ball bounces up half the previous height it fell. If a rubber ball is dropped from a height of 20 feet, what is the height the ball bounces on the nth bounce?

5. Chain Letter Problem. You send out 7 letters to different people on the first day. On the second day, each of the 7 people send out 7 more letters to new people. The process continues for several days. How many letters will be sent on the d-th day?

6. A bacteria cell can divide into two identical cells after 1 minute. Each of the new cells can also divide after 1 more minute. If each cell can divide every minute, how many cells are there after one hour? Write an expression for the number of bacteria cells after t minutes.

7. A tennis tournament begins with 128 players. After the first round 64 teams remain, After the second found, 32 teams remain. How many teams remain after the third, fourth, and fifth rounds? How many rounds will it take before there is a winner? Write a finite sequence that represents the number of teams that have been eliminated after r rounds of the tennis tournament. What is the domain of r?

Quadratic

8. Diagonals are formed on regular polygons, starting with a three-sided regular polygon or equilateral triangle. The variable n represents the number of sides in the polygon. Determine the number of diagonals in a regular polygon with 20 sides. Then determine the equation for the number of diagonals in a regular polygon of n sides.

9. Round-Robin Tournament (Variation of Handshake Problem). In a round-robin tournament, each team plays each other team only once. Starting with two teams, create a sequence with five terms to show the relationship between the number of teams in a round robin tournament and the number of games that need to be scheduled. Write a function to determine the number of games if there are t teams.

10. Double Round-Robin Tournament. In a double round-robin tournament, each team plays each other team twice. Starting with two teams, create a sequence with five terms to show the relationship between the number of teams in a round robin tournament and the number of games that need to be scheduled. Write a function to determine the number of games if there are t teams.

11. Triple Round-Robin Tournament. In a triple round-robin tournament, each team plays each other team three times. Starting with two teams, create a sequence with five terms to show the relationship between the number of teams in a round robin tournament and the number of games that need to be scheduled. Write a function to determine the number of games if there are t teams.

12. How many regions are there in the plane cut out by n lines in general position (meaning, no two parallel, no three concurrent)

13. Find the sum of the first n odd positive integers.

Other

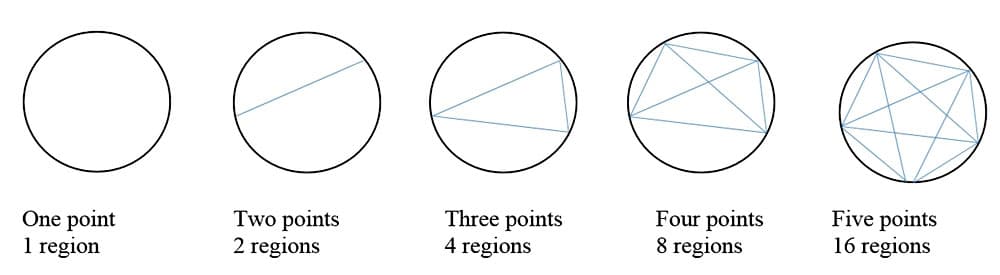
14. Partitioning of a Circle Problem. Given a circle, begin with one point on the circle. Add a point on the circle and draw a chord connecting all points. Count the number of partitioned regions in the circle. Add another point and draw chords connecting the new point to all existing points on the circle. Again, count the number of regions partitioned in the circle. Continue the pattern and record the number of partitioned regions.

15. Fibonacci Sequence {1,1,2,3,5,8,….}

16. Cubed Numbers. {1,8,27,64,…}