From Arithmetic to Algebra: Variables, Word Problems, Fractions and the Rules

Content Objectives

Overview

If you have 4 pencils and I have 7 apples, how many pancakes will fit on the roof? Purple, because aliens don’t wear hats.¹

This is a meme that I have encountered in various forms on social media, and even from students joking around in person. Word problems seem to be a commonly cited justification for hating math, particularly algebra. Jokes aside, in my experience as a secondary math teacher, even students who are skilled in solving given algebraic equations struggle in creating their own equation to solve a word problem. This is not so surprising, because the demands of solving an equation are very different from the demands of formulating an equation from a verbal or written context. To formulate an algebraic equation that correctly represents a situation, students must interpret a verbal or written statement, and symbolically represent the relationship of its parts. Thus, to improve student success with formulating algebraic equations, we must provide instruction in both the process of decoding a problem, and using mathematical notation that maintains the meaning of the original problem.

The purpose of this curriculum unit is to help students translate word problems into first order equations that can be written in the form ax + b = c. For purposes of this unit, a, b, and c will be whole numbers. To do this, I will help students identify and organize the given information, the unknown value, and the relationship of the values of the problem through verbal discussions and visual models. By organizing this information, students will have an easier time representing these quantities and relationships symbolically. In the long run, I hope this curriculum unit also gives my students confidence to approach more complicated word problems as they progress further in math.

This unit is the first of four complementary curriculum units developed in the 2017 Yale National Initiative (YNI) math seminar, “From Arithmetic to Algebra,” about translating, simplifying, and solving algebraic expressions and equations. For the rest of the related curriculum units, please see the work of 2017 math Fellows Jeffrey Rossiter, Xiomara Pacheco, and Sally Yoo. (See Figure 1 below, which summarizes the connection between the concepts of our pieces.)

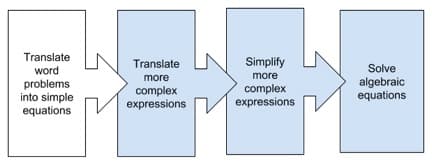
Figure 1

This order is surprising because, in most textbooks, translating and simplifying algebraic expressions comes first, followed by solving equations, and ending with word problems. However, starting with word problems provides the motivation for using algebraic notation to represent increasingly complex situations. While bar models are useful in representing, and even solving simple word problems, students will need more sophisticated skills in representing and manipulating equations with compound expressions. Therefore, the intention of this curriculum unit is to merely begin a broader investigation into algebraic expressions and equations, which may last for an entire semester.

Rationale

I teach at Peter Burnett Middle School in San Jose, California. Currently, Burnett Middle School’s overall math performance on the California Assessment of Student Progress and Performance (CAASPP) falls well below the state average.² Last year, 13% of Burnett’s students met or exceeded standards, compared to a 37% statewide average. Since CAASPP results are one of the measures used in course placement in my district, I worry that these scores will limit students’ opportunities to take algebra 1, and serve as indicators of their likelihood to succeed in that course. Moreover, having taught or tutored every higher-level course from geometry to calculus, I know that algebra skills are necessary to take and succeed in each of these classes as well. So very few of Burnett’s students are on track to take any of these higher-level math classes, which will limit their opportunities in college. Colleges will want students to take remedial math, which may lead to falling behind in their other courses, and hindering their path to a diploma. Even those who go directly into the workforce, or training outside of higher education, may be affected. Among high school graduates who don’t attend college, “those with low levels of math are 50 percent more likely to be unemployed than those with higher levels of math, and they typically earn about $ 1.30 less per hour.”³ So while the CAASPP itself is a single test, what the scores reveal about math competence among Burnett students can have much longer-lasting repercussions. The goal of this unit is to improve my students’ algebra skills, and consequently, their future opportunities.

This curriculum unit targets students in 7^th grade math, which covers pre-algebra concepts and skills. Similar to whole school performance stated above, 13% of Burnett 7th graders met or exceeded math standards on the CAASPP, compared to 36% statewide. This number covers all 7th graders, including those who are in an additional math support course, those who are “on grade level”, and those who are in advanced placement (7th grade accelerated, or Algebra 1). My curriculum unit will focus on students “on grade level” who, despite that classification, underperform on district benchmark exams. Fewer than 1 in 25 of my 55 “grade level” students were proficient on the 2016-2017 exam on my district’s Algebraic Expressions and Equations, which assessed using variables to represent real-world quantities, and formulate simple equations to solve those problems. (See APPENDIX A for full list of standards.) The primary objective of this unit will be to equip students with the tools to interpret a word problem, and to write an algebraic equation that accurately relates its quantities.

In the 2016-2017 school year, my district started using the Springboard Course 2 Textbook for 7th grade math; in this book, there is only one lesson on “Modeling and Writing Two-Step Equations”. After teaching this lesson, I have concluded that it has several deficiencies. First, the lesson over-scaffolds the translation process, by providing a numeric expression to represent the word problem, and by defining the variable for students. Then, the lesson over-simplifies the distinction between an equation and an expression. Specifically, equations “have an equal sign”, and expressions do not. Finally, the lesson introduces vocabulary, such as “coefficient” and “constant”, without connecting back to the word problem. As a result of these shortcomings, students do not get enough practice in creating the structures of the expression or equation themselves, including operations, or in creating appropriate notation for unknown values.

6th grade standards also cover some of the skills needed in translating situations into expressions or equations. By 7^th grade, students should already know how to use variables to represent unknown numbers, and write expressions and equations to solve real world problems; specifically, in the 6^th grade, students practice problems that can be written as one-step addition or multiplication equations. (See APPENDIX A for full list of standards.)

When I taught 6th grade math in 2015-2016, I used my own worksheets to instruct students on identifying “key words” when translating verbal sentences into algebraic expressions and equations. For addition, I gave the words increase, more, sum, and deposit. For subtraction, the words/phrases were difference, decreased by, less than, and withdrawal. For multiplication, I gave times and product. I indicated division by quotient. And for equal, I gave the word is, and the phrase the same as.

However, both in my experience, and according to cognitive research,⁴ this type of syntactic—or word-by-word—translation directly leads to many misconceptions and mistakes. Students often made reversal errors, as when translating “four less than a number” to “4-x,” rather than “x-4.” Moreover, as my lists were not exhaustive, students struggled when translating word problems with unfamiliar words indicating operation, such as “each” in, “There were 56 students in a room, arranged in 4 rows. How many students were in each row?”  Even the key words that I have listed can have multiple meanings, depending on the context. If I say, “Andrew had three cookies, then bought two more,” this indicates addition, whereas, “Andrew has three cookies, which is two more cookies than Robert has,” indicates subtraction. These examples illustrate Polya’s⁵ comparison of translating a word problem into an equation, to translating between English and French, which requires understanding the English sentence, knowing the forms of expression specific to French, and being familiar with idiomatic expressions that cannot be translated word-for-word. Similarly, we must be familiar with rules and notation specific to mathematical representation, and focus on whole meaning rather than word-for-word translation from a word problem. I am confident that I have not been alone in using the key word approach. Thus, 7th graders in 2016-2017 may have come in with prior misconceptions about translating word problems to expressions or equations.

For the 2017-2018 school year, my rising 7th graders will be the first class that used the Springboard curriculum in 6th grade. Their Course 1 textbook has more material on formulating algebraic expressions and equations on “Writing Equations”, “Representing Situations with Equations”, and “Modeling and Solving Addition, Subtraction, and Multiplication Equations”.

“Writing Expressions” has the same syntactic format as my own lesson on identifying key words, thus enforcing the same misconceptions. However, the given examples focus on translating verbal phrases such as “12 less than twice a number,” without instruction on how to transition to meaningful word problems. So students lack guidance in considering how context and phrasing of a real world problem affect the structure of the equation. This lesson also asks students to “simplify” or show “equivalence” between expressions, prior to any lessons on how to simplify, or what equivalence means. It would be better to discuss these terms when students actually encounter a situation that can be represented by multiple expressions; this way, both the process of simplifying, and the concept of equivalence will have applied meaning to the students. 

“Representing Situations with Equations”, like the lesson in Course 2, over-scaffolds by providing the structure of the equation, rather than having students derive it themselves. Again, there is also little instruction about transitioning from purely verbal phrases to word problems that represent an actual situation. Thus, students lack guidance in semantic, or conceptual, understanding of word problems. Similar issues repeat themselves in the remainder of the lessons named above, although they do provide actual contexts to translate.

Key Ideas

In the 2017 YNI math seminar, we examined the Common Core State Standards (CCSS) taxonomies for one-step equations⁶ by looking at a given context, examining which problem type is represented, and how the equation for that context changes, depending on what is given, and what is unknown. However, I worry that having students memorize the problem types will essentially be the same as having them memorize key words. Instead, I want the students to learn how to carefully read each problem, and critically think about the data, the unknown values, and the relationship between the values. To scaffold this process, I will use visual models, based on the bar models from the Singapore Bar Method, as described below. While some students will be able to translate a word problem directly into symbolic terms, visual models may assist struggling students, and may help all students with more complex problem types. Additionally, students who are able to write an equation directly from a word problem may use Singapore bar models to check consistency between the relationship represented in the equation and the relationship represented in the word problem.

Singapore Bar Models to Categorize Problems

The Singapore Bar Method scaffolds the process of translating word problems by requiring students to identify and organize the unknown information, the given data, and the condition(s) relating these values in a single model. Thus, students are using a visual means of answering Polya’s guiding questions in understanding “Problems to Solve.” ⁷ Furthermore, the process of answering these questions pushes students to conduct multiple reads of a word problem. “The first reading provides the context of the story. In subsequent readings of the text, information is further processed to ascertain what the givens are and what is to be found.”⁸ Additionally, a collaborative paper between a neuroscientist and math educators references multiple studies, anecdotal information from teachers, and neuroimaging to link math performance and use of visuals.⁹ So along with the specific information bar models prompt and convey, using visual representations may help students, and raise math achievement, in general.

The way that students will set up a bar model will depend on the type of problem to be represented. Practice with providing the models for these one-step equations should prepare students to use them to then model multi-step equations. I can assign the various one-step problems to four types of bar models: Part-Whole, Comparison, Multiplication and Division, and Multiplicative Comparison. The first three models are those identified in resources I have encountered on the Singapore method.¹⁰ The last is a combination of the Comparison and Multiplication and Division models. As I describe the problem types that apply to each bar model, I will refer to the CCSS taxonomies, which I have adapted in the table below. However, as I mentioned above, I do not plan to teach the students this language.

Selected CCSS Problem Taxonomies

I have modified some of the terminology of the taxonomies about the problem types and their parts. Instead, I will use alternative language we used during the YNI seminar, as it better describes the situations that apply to a specific problem type. For example, the problems I label as “Part-Part-Whole” are called “Put Together/Take Apart” in the CCSS guide. However, in the example situation about the red and green apples, you really aren’t putting anything together, as both types of apples are already there. It is more accurate to think of red apples and green apples as being parts of a whole group of apples. Also, the CCSS guide identifies the components of “Compare (Multiplication/Division)” problems as Number of Groups • Group Size= Product. However, I find that the language of Factor • Smaller = Bigger better matches the “Compare (Addition/Subtraction”)” language. (For a more in-depth explanation, see Multiplication & Division Models section below.)

I am purposely skipping problems based on the Array category in the taxonomy, because I did not come across many problems that require arrangement into rows and columns. Also, since the Singapore Bar Method relies on a linear model, rather than an area model, it is not ideal when approaching these types of problems.

(For the example situations with various unknown and given quantities, please see the CCSS guide for math, pp.88- 89.)

Addition/Subtraction Models

Part-Whole Models show a bracket as equal in length to a pair of bars, which indicates that the large one has the same value as the two small ones combined. This is how addition is realized in the domain of length measurement. These can, of course, be applied to “Part-Part-Whole” problems, which can be written as Part + Part = Whole. With this first model, I will discourage my students from making equal parts, unless this is specifically stated in the problem, as they may be tempted to simply divide a quantity by two if they draw the small bars the same length. Alternatively, introducing obviously different quantities may help students see this themselves. (See Figure 2 below.)

Figure 2

For example, “Sandy's high school played 14 hockey games this year. The team won most of their games. They were defeated only in 4 games. How many games did they win?” (The model for this is in Figure 3 below.)

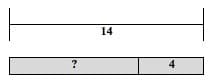
Figure 3

The bracket above indicates the total number of hockey games, the “?” represents the number of games that her team won, and the 4 represents the number of games that the team lost. (See APPENDIX B and Teacher Resources for more example problems.) Although this model follows the order of the parts listed in the word problem—that is, “games won” in the leftmost bar, and “games lost” in the rightmost—this type of problem may be useful in introducing the commutative property of addition. This discussion would come naturally from students who draw the bars in the opposite order.

The diagram for the Part-Whole Model can also be applied to “Add to” and “Take from” problems, labeled appropriately for each problem type. Although these are distinguished in the taxonomy from “Put Together/Take Apart” problems, this model captures well any one-step problem with an additive relationship. It can also be applied to comparison problems.

For “Add to” problems, we will use the convention of labeling the leftmost bar as the Start, the rightmost bar as the Change, and the bracket as the Result. For example, “There were 8 roses in the vase. Melanie cut some more roses from her flower garden and added then to the vase. There are now 17 roses in the vase. How many roses did she cut?” (See Figure 4 below.)

Figure 4

The bracket above indicates how many roses are in the vase now, the 8 represents the roses that were in the vase before Melanie cut roses, and the “?” represents how many roses Melanie cut from her garden.

For “Subtract from” problems, we will label the bracket as the Start, the leftmost bar as the Change, and the rightmost bar as the Result. For example, “Tom received 80 dollars for his birthday. He went to a sporting goods store and bought a baseball glove, baseball, and bat. He had 39 dollars left over, how much did he spend on the baseball gear?” (See Figure 5 below.)

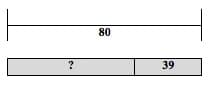
Figure 5

The bracket above indicates the amount of money Tom received for his birthday, the “?” represents how much he spent on baseball gear, and the 39 represents how much money he had left. (See APPENDIX B and Teacher Resources for more example problems.)

Comparison Models apply to “Compare (Addition/Subtraction)” problems, which can be written as Smaller + Difference = Bigger. (See Figure 6 below.)

Figure 6

The bars in this model are stacked vertically in order to show the size of one value in relation to the other values. For example, “Connie has 15 red marbles and 28 blue marbles. How many more blue marbles than red marbles does Connie have?” (See Figure 7 below.)

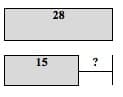
Figure 7

Although 15 red marbles are mentioned first in the word problem, students should figure out that the bigger amount, 28 blue marbles, should be the top bar, with the “?” symbol labeling the bracket, and representing how many more blue marbles Connie has, compared to the number of red marbles she has. Deciding on the correct relationships is the core of understanding the problem. The construction of bar models provides a structure to help students work through this process. (See APPENDIX B and Teacher Resources for more example problems.)

Multiplication/Division Models

Just as multiplication can be viewed as repeated addition of equal parts, the Multiplication and Division Model can be viewed as an extension of the Part-Whole Model. This model applies to “Equal Group” problems that can be written in the form Number of Groups • Group Size = Product. (See Figure 8 below.)

Figure 8

As you can see, the generalization of this model is a bit more abstract than the Part-Whole Model. This is because, without knowing how many groups there are, we are unable to draw the correct number of equal parts. Instead, we use ellipses to represent a continuation of bars of equal size between the first and last bars that are drawn in. We can also use ellipses to represent a large number of groups that would be too tedious to draw in our model. A “large number” is subjective, and will be different according to the person using the model, but one book recommends to use “this approach when multiplying by a factor greater than 10.”¹²

Here is an example of the same situation, with different unknown values. Notice how the model changes, depending on whether number of groups is unknown or group size is unknown.

“At a restaurant, Mike and his three friends decided to divide the bill evenly. If the total bill was $ 52, how much did each person pay?” (See Figure 9 below.)

Figure 9

In this example, the unknown value is the group size, as indicated by the “?” inside each of the equal groups. This is fairly straightforward to illustrate using a bar model.

In contrast, consider the situation written as, “At a restaurant, Mike and some of his friends decided to divide the bill evenly. If the total bill was $ 52, and each person paid $ 13, how many people divided the bill?” (See Figure 10 below.)

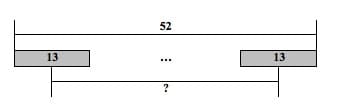
Figure 10

Here, we know that the group size is 13, representing the $ 13 that each person paid, but we don’t know the number of groups, which represents the number of people who split the bill. As mentioned in the general model, since we don’t now how many equal groups to draw, we use ellipses to indicate the continuation of the same sized group between the two that are illustrated. (See APPENDIX B and Teacher Resources for more example problems).

Finally, the Multiplicative Comparison Model combines aspects of the Comparison Model the Multiplication and Division Model. This model applies to “Compare (Multiplication/Division)” problems, which can be written in the form

Factor • Smaller= Bigger, for whole number factors. However, if a factor is between 0 and 1, then Factor • Bigger = Smaller would be an accurate statement. For example, “Tanya had half as many red toy trucks as Al” could be represented in the equation, ½ a = t, where a is the number of red toy trucks Al has (the Bigger amount), and t is the number of red toy trucks Tanya has (the Smaller amount). However, this curriculum unit will focus on cases wherein the multiplicative factor is a whole number. So, to attack this  problem, I would ask my students to convert it into a comparison of Al to Tanya, rather than the other direction, and to write the equation a = 2t. This can then be handled nicely with a bar model similar to the one illustrated in Figure 9 above.

Although the CCSS guide uses the same language as the “Equal Group” problems, I am using the more descriptive names, “smaller” and “bigger” to mirror the language in the “Compare (Addition/Subtraction)” problems. (See Figure 11 below.)

Figure 11

As with the Comparison Model, the bars in this model are stacked vertically in order to show the size of one value in relation to the other value. Further, as with the Multiplication and Division Model, in order to represent the number of groups, we use ellipses in the general model, when the number of groups is unknown, or when the number of groups is too large.

For example, “A bus is 45 feet long. It is 3 times as long as a car. How long is the car?” (See Figure 12 below.)

Figure 12

The 45 represents the length of the bigger vehicle, and as you can see, the bar is three times the length of the smaller bar, the length of which is represented by “?”. The quantities throughout the model are in feet. (See APPENDIX B and Teacher Resources for more example problems.)

It is worth noting that this type of word problem is another common source of reversal errors. For example, for the situation “6 times as many students as professors,” students are likely to write the equation “6S=P,”¹³ with S representing the number of students, 6 as the Factor relating the number of students and professors, and P representing the number of professors.

However, we could construct a bar model. (See Figure 13 below.)

Figure 13

Here, the number of students, represented by S, is equivalent to 6 times the number of professors, represented by P. Also note here that, rather than using a “?” to represent an unknown value, I used the variables themselves. As students become more comfortable with the use and meaning of variables, I will encourage them to make that transition as well.

However, this model can be a source of confusion in and of itself. There is only one S, and 6 Ps; does this mean, therefore, that there are more professors than students? Before I answer this question, it may be useful to review some common proportional relationships—or multiplicative comparisons—through the lens of unit conversions.

Proportions as Multiplicative Comparisons

There are 3 feet in 1 yard, which can be written as the ratio, 3 feet/1 yard =1. However, you want to know the number of yards you have, Y, if given F number of feet, it is better to write this relationship as a multiplicative comparison. It would be tempting to write 3F=Y, as this equation matches almost word-for-word with the sentence, “there are 3 feet in 1 yard.”

Yet, if we add units into the equation, we can see why it is incorrect.

3feet/yard∙F feet=Y yards simplifies to 3 F feet²/yard=Y yards.

Therefore, the units are not compatible.

Instead, if we make 3 the coefficient for Y, we get 3feet/yard∙Y yards =F feet, which simplifies to 3Y feet=F feet, which will make sense in standard numerical form, 3Y=F.

To clarify this point further, it may be helpful to repeat the reasoning above using other commonly known unit conversions, such as “12 inches in 1 foot”, “60 minutes in 1 hour”, and “7 days in 1 week”. All of these example illustrates how objects in multiplicative comparison problems have an inverse relationship between the number of units and the size of the unit. That is, because there are 3 feet in a yard, you must multiply 3 by the number of yards (the larger unit) to get the number of feet (the smaller unit); this means that there is a larger number of the smaller unit, and a smaller number of the larger unit.

Thus, revisiting the student and professor example in the previous section, “6 times as many students as professors” can be also thought of as the ratio 6 students/1 professor . The correct equation, therefore would look like:

(6 students/professor)∙ (P professors)=S students

This simplifies to 6P students = S students. Since the units are the same, the equation will still make sense in standard numerical form, or 6P=S. Saying that there is one professor for 6 students is parallel to saying that there is one yard for 3 feet. “Professor” is functioning as the larger unit, and “student” as the smaller. Hence the number of students must be 6 times the number of professors.

Transitioning from Models to Algebraic Equations

The next step for students using a visual model to transition into writing an equation is to introduce suitable notation.¹⁴ The two parts that students often struggle with are where to place the “=” symbol, and how to use a variable.

Another benefit of using visual models prior to writing equations is that it emphasizes the relational meaning of the “=” symbol, as opposed to the operational meaning. “Operational meaning stands for the...asymmetric use: ‘operation equals answer,’ which is often described for elementary arithmetic…Relational meaning focuses on a symmetric use of the equal sign.”¹⁵

Since the sizes of bars and brackets show the relationship between the values in the models, it is easier to understand why a given situation represents an equation rather than an expression. Looking at the bus example for the Multiplicative Comparison Model, each bar is its own expression. The top bar represents one quantity (the length of the bus, in feet), and the bottom bar represents another quantity (the length of the car, in feet). Since the top bar is comprised of three copies of the bottom bar, the length of the bus is the same as three times the length of the car, or the length of the bus “=” three times the length of the car. Therefore, the relationship of the quantities in the bar models helps you can see an equation relating two expressions, or the lengths of the different vehicles

Regarding variables, there is a common misconception of “symbols as labels that can shift within an activity; for example…b = books, which can be interpreted later as the number of books, the value of the book, the value of the total number of books, etc.”¹⁶ To avoid this, I will model and reinforce the need to identify the unknown value as a number with appropriate units.¹⁷ I will make sure that my students develop the habit of specifying the units of their variables.

It may be useful for struggling students to identify the units of all of the parts of a problem. Additive problem types should have the exact same unit for each of its parts, in order for the addition to make sense in standard numerical form. Multiplicative problem types are a bit more challenging, as each factor may have different units, but, once multiplied, should result in the same unit on both sides of the equation. The models themselves are one means of checking that units correspond. In the additive case, in the Part-Whole Model example on Sandy’s hockey team, although one part is “number of games lost,” and another part is “number of games won,” these parts are both a certain number of the unit “game,” which is also the unit of the “total number of games.” Meanwhile, in the Multiplication and Division example on plums divided among bags (see Classroom Activities), if you multiply the number of groups "number of bags of plum," by the group size, "number of plums per bag", the product will be the total number of plums.

I expect that even students who can directly translate word problems into equations without the help of bar model(s), by explicitly identifying units for variables and known values alike, will have an easier time verifying that their equation makes sense when they solve a problem arithmetically, using the corresponding model. Can you combine the units in the equation in a way that is compatible with the situation? Does the solution match the magnitude and the units of the context? This last check also reinforces students’ conceptual understanding of the word problem as a whole, and the connection between the word problem, visual model, and equation.

Once students understand how to categorize one-step word problems by bar model type, represent the problem using the appropriate bar model, and translate those models into equations, they should be ready to put those pieces together to categorize and symbolically represent multi-step situations.

Introducing Inverse Operations

Along with providing a scaffold for translating word problems into equations, Singapore Bar Models can help with introducing the concept of inverse operations. “By a process of undoing, the value of the unknown [quantity] is found. Hence, children [using bar models] circumvent the cognitive demands that are inherent in solving algebraic equations, which normally require the construction of a system of equivalent equations.”¹⁸ In the Part-Whole Model examples in the previous section, the models represent additive relationships. However, to figure out the missing value in each of these examples, students must actually subtract, which is the inverse operation of adding. The diagram helps them understand what to do. Similarly, the Multiplicative Comparison Model example represents a multiplicative relationship. But in order to solve this problem, students should divide, which is the inverse operation of multiplying. By providing a visual wherein students can literally take away part of an amount, or split up an amount, use of bar models makes students less likely to perform the wrong operation, even when it is suggested by a “key word” (for example, getting r = 25 for 8 + r = 17 by adding 8+17).

Similarly, a bar model representing a two-step equation can help justify the convention of removing the constant prior to the coefficient. Below, I am using a combination of a Part-Whole Model and a Multiplication and Division Model to represent the general form of a first order equation in one variable, ax + b=c. Using the structure we have established for the Part-Whole Model, ax will be the first Part and b will be the second Part of the model. Then, using the structure of the Multiplication and Division Model, a will represent the number of groups, and x will be the group size. (See Figure 14 below.)

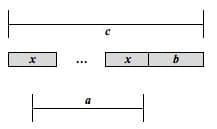
Figure 14

Using the model, you would first subtract b from c to be left with a groups with equal, unknown size, x. To figure out the value of x, divide the new amount (c-b) by a.

Symbolically, this looks like

ax + b=c

ax + b – b = c – b

ax + (b – b) = (c – b)

ax + 0 = (c – b)

ax = (c – b)

ax/a=(c-b)/a

1x=(c-b)/a

x=(c-b)/a

Thus, bar models can help students both translate word problems into equations, and introduce them to aspects of solving these equations algebraically.