From Arithmetic to Algebra: Variables, Word Problems, Fractions and the Rules

Classroom Activities

Preparing for the Unit

Prior to teaching the different models to students, I plan to give students a short pre-assessment on simple word problems. A sample task on this pre-assessment is this matching activity.

Students should correctly identify:

1. C
2. A
3. B

I will then ask students to verbally explain how they matched each word problem with its respective equation. In this way, I can see what intuition students already have about translating real world situations to symbolic representations.

Sequence of Content

I will instruct students in the different bar models and their corresponding problem types, according to complexity of the model.

1. Part-Whole Model
2. Comparison Model
3. Multiplication and Division Model
4. Multiplicative Comparison Model
5. Combining Model Types

I will teach the Part-Whole Model first, as it is needed to later understand the Multiplication and Division model. Similarly, both the Multiplication and Division Model, and the Comparison Model are needed to represent “Compare (Multiplication/Division)” problem types. Of course, it is necessary to learn all of the models for the one-step problem types, before representing multi-step situations.

For each new bar model, and when we first combine models, I will introduce a word problem that will produce the desired model. For each problem type applied to the model, I will ask: How do you set up the model? What is the unit of each piece of the model? What is the unknown value, and its unit, and what variable will you use? How can you represent each part of the model in an equation? What is the solution to the situation (either using the model or the equation)? Check that the solution makes sense for the units and the magnitude of the situation If you change what is unknown in the word problem, how does that change the model and the equation?

Below, find a one-step example, a two-step example, and a multi-step example. (See APPENDICES B-F for more examples.) Note that I will not have students change the unknown in the multi-step word problem.

One Step Equations

1) Word Problem: If 18 plums are shared equally into 3 bags, then how many plums will be in each bag?

Model Type(s): Multiplication and Division Model

Bar Model: (See Figure 16 below.)

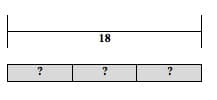
Figure 16

Algebraic Equation:

? = the number of plums in each bag = p

3p = 18

State & Check your Solution:

There will be 6 plums in each bag, because 3bags of plums•(6 plums per bag) =18 plums.

2) Word Problem:

If some plums are shared equally into 3 bags, and there are 6 plums in each bag, how many plums are there in total?

Model Type(s): Multiplication and Division Model

Bar Model: (See Figure 17 below.)

Figure 17

Algebraic Equation:

? = the total number of plums = t

3•6 = t

State & Check your Solution:

There will be 18 plums total, because 3 bags of plums•6 plums per bag =18 plums.

3) Word Problem:

If 18 plums are shared equally into some bags, and there are 6 plums in each bag, how many bags are there?

Model Type(s): Multiplication and Division Model

Bar Model: (See Figure 18 below.)

Figure 18

Algebraic Equation:

? = the number of bags of plums = b

b•6 = 18

State & Check your Solution:

There will be 3 bags of plums, because (3 bags)•6 plums per bag =18 plums.

Two Step Equations

1) Word Problem: Oceanside Bike Rental Shop charges a 12 dollar fixed fee plus 7 dollars an hour for renting a bike. Fred paid 54 dollars to rent a bike. How many hours did he pay to have the bike checked out?

Model Type(s): Part-Whole Model, Multiplication and Division Model

Bar Model: (See Figure 19 below.)

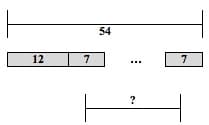
Figure 19

Algebraic Equation:

? = the number of hours he had the bike checked out=h

12+7h = 54

State & Check your Solution:

Fred paid to rent the bike for 6 hours, because $ 12+$ 7 per hour•(6 hours) = $ 12+$ 42 = $ 54.

2) Word Problem: Oceanside Bike Rental Shop charges a fixed fee plus 7 dollars an hour for renting a bike. Fred rode for 6 hours, and paid 54 dollars to rent a bike. How much did Fred pay for the fixed fee?

Model Type(s): Part-Whole Model, Multiplication and Division Model

Bar Model: (See Figure 20 below.)

Figure 20

Algebraic Equation:

? = the amount Fred paid for the fixed fee, in dollars=f

f+7•6 = 54

State & Check your Solution:

Fred paid a fixed fee of $ 12 because ($ 12)+$ 7 per hour•6hours = $ 12+$ 42 = $ 54.

3) Word Problem: Oceanside Bike Rental Shop charges a 12 dollar fixed fee plus some dollars an hour for renting a bike. Fred rode for 6 hours, and paid 54 dollars to rent a bike. How much did Fred pay per hour of renting the bike?

Model Type(s): Part-Whole Model, Multiplication and Division Model

Bar Model: (See Figure 21 below.)

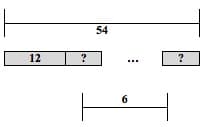
Figure 21

Algebraic Equation:

?=amount Fred paid per hour of renting the bike, in dollars=p

12+p•6 = 54

State & Check your Solution:

Fred paid $ 7 per hour to rent the bike, because $ 12+($ 7 per hour)•6hours = $ 12+$ 42 = $ 54. (See APPENDIX B and Teacher Resources for more two-step word problems)

Multistep Equations

1) Word Problem: Divide $ 79 among three people so that the second will have three times the amount of the first, and the third will have two dollars more than the second

Model Type(s): Part-Whole Model, Multiplicative Comparison Model, Comparison Model

Bar Model: (See Figure 22 below.)

Figure 22

Algebraic Equation:

?=the amount of money the first person gets, in dollars=f

f+(3f)+(3f+2) = 79

7f+2 = 79

State & Check your Solution:

The first person will get $ 11, because ($ 11)+(3•$ 11)+(3•$ 11+$ 2)= $ 11+$ 33+($ 33+$ 2)= $ 44+$ 35= $ 79.

It is worth noting that this last problem is quite complex, as it requires adding three unknown values. Using bar models makes this problem more manageable, and should help students see that they need 7 copies of the unknown, and then $ 2 more, even if they are not comfortable with “adding like terms”. However, as mentioned in the overview, students will later encounter problems that require more sophisticated methods of translating and solving. (See APPENDIX B and Teacher Resources for more multi-step word problems).

Once students have shown proficiency in problems of at least two model types, I will provide a mix of word problems. Students will then determine:

• What is the structure of this problem, and what is it asking?
• What model do you need?

Then they will then continue the process outlined in the examples above to represent each word problem as algebraic equations.

Student-Created Word Problems

Up to this point, I have given students a word problem, and they have been creating a model—or combination of models for multi-step problems—and an algebraic equation that represent the situation. Next, I would give students either an algebraic equation or a visual model, and ask them to create a word problem that matches the given representation. Then I will have them explain why the equation or model accurately represent the word problem they have created.

A given equation: Create a word problem that can be represented as 2x+3=9

A given model: Create a word problem that can be represented by the model (See Figure 23 below.)

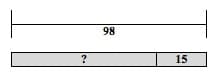
Figure 23

Once students have practiced creating a word problem that matches a specific model or equation, I will have them come up with an original word problem. Then, they will

1. Represent the word problem using an appropriate bar model (or combination of bar models);
2. Define the variable, with appropriate units, and write a corresponding algebraic equation;
3. Explain how the word problem, model, and algebraic equation match; and
4. Rewrite the word problem with the same situation and amounts, but with a different quantity for the unknown value;
5. Determine how the new unknown value effects the other representations of the situation.

This will be one of their summative assessments, completed in groups, in addition to a more traditional individual paper-and-pencil test.