Teaching Strategies
Assessing through an International Baccalaureate Lens
As an International Baccalaureate (IB) school,19 Burnett grades students in each subject on a scale from 1-8 across four different criteria in a subject. Therefore, rather than having a single grade that summarizes a students’ mastery of math as a whole, I can assign four scores on their knowledge of math skills and concepts, investigation of patterns, communication, and application of math in real-life contexts. In addition to breaking down the subject into four criteria, each score comes with a descriptor that provides qualitative feedback for the student and parents. For this curriculum unit, I will assess students using Criterion C and Criterion D. (See Teacher Resources for criteria rubrics.)
Criterion C, Communicating: Students use appropriate mathematical language and different forms of representation when communicating mathematical ideas, reasoning and findings, both orally and in writing.
For Criterion C, students will represent the information in a word problem using models, symbols, and words. Within their equations, I will check that students clearly define their variables as numbers, with appropriate units. I will also give students opportunities to create a bar model, an algebraic equation, or a word problem when given one of the other representations, as well as the opportunity to create their own original word problem, using all of the mentioned representations. Throughout the curriculum unit, I will require students to write and/or discuss how the model, equation, and word problem all show the same values and relationships.
Criterion D, Applying Mathematics in real-life contexts: Students transfer theoretical mathematical knowledge into real-world situations and apply appropriate problem-solving strategies, draw valid conclusions and reflect upon their results. For Criterion D, students will be engaging with real-life contexts presented in word problems. Applying appropriate problem-solving strategies will require writing a correct equation, which may include choosing the correct bar model to represent a situation. Then, after solving either arithmetically or algebraically, students will reflect whether their solution is reasonable for the given context. This includes checking that the units of each part of the equation correspond, and that they make sense after calculation.
Thus, assessing students using Criteria C and D will push me to frame each class activity around using multiple mathematical representations to understand and solve word problems from a variety of contexts. Additionally, having students use the criteria rubrics to self-assess and assess and their peers, they will gain practice on critiquing their own representations—models and/or equations—and the reasonability of their solutions in context of a given word problem.
Explicit Direct Instruction (EDI) with Graphic Organizers
When introducing each new model, and the idea of combining models, I plan to use EDI, consisting of orientation, gradual release (teacher-led, collaborative, then independent problem-solving), and closure. As students will be responsible for multiple representations of a problem, I will provide graphic organizers for students to record each word problem’s model type, the bar model itself, and the resulting algebraic equation with a defined variable and unit. This graphic organizer will mirror the questions that students should ask themselves when translating between representations. (See Figure 15 below.)
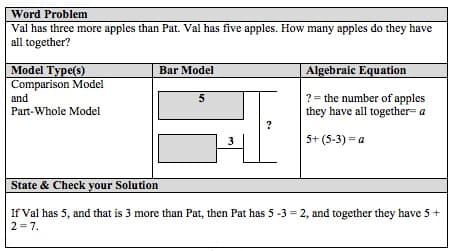
Figure 15
(See APPENDIX C for a blank template of the graphic organizer.)
Just as the bar method itself is merely a scaffold as opposed to an end in and of itself, the graphic organizer is merely a helpful tool that students should not rely on. Instead, I hope that students can find their own way to identify important aspects of a word problem, and to organize their multiple representations. The graphic organizer is just to get them started.
Think-Write-Pair-Share
A strategy I will use within the EDI framework is giving students individual time to work on a translation problem, record their thoughts, and then discuss with a partner. One thing that I do, in particular, is create different student pairings so that students can hear from multiple perspectives. There is the usual pairing of speaking to the student sitting next to you (“elbow partners”) or across from you (“face partners”), but I have also had students go to a corner of the room, corresponding with the colored sticker on their desks, and other pairings that will also require students to get up and move. To keep each student accountable, I will then call on a non-volunteer to share his or her solution to the whole class, and the rest of the class would verify this solution. Peers may ask specific clarifying questions, or they may help the student sharing if they believe that the solution was incorrect. This would also be an opportunity for broader whole-class discussion on the translation process.
Structured Student Groups
In addition to collaborating during direct instruction lessons through Think-Write-Pair-Share, students will have opportunities to collaborate for more sustained periods through structured group work. To facilitate team interdependence, I will assign group roles20 of Facilitator/Timekeeper, Recorder, Errand Monitor/Presenter, and Summarizer (see Teacher Resources for link to role descriptors.) To balance teamwork and individual accountability, I will assess students as a group, as well as individually; students will have an opportunity to grade themselves, as well as their group mates.
I will use structured group work for activities that require a final product that will be shared either as a presentation, or through a gallery walk21. This may include activities where students must create their own word problem, given either a model or an algebraic equation, or showing how changing what is unknown in a context will change the model and algebraic equation.

Comments: