Surface Area
In this topic, we are finding the surface area of three dimensional objects or the total area of the outside surface of a 3-D shape. A net is a mathematical tool used by many educators to help students in learning the concept of surface area. A net is a 2-dimensional pattern shape that can be folded to form a 3-dimensional shape or a solid. In other words a pattern made when the surface of a three-dimensional figure is laid out flat showing each face of the figure, which the students will use to find the surface area of the three dimensional figures.
First students should understand the use of nets with two-dimensional shapes which relates to the concept of finding area using graph paper. By using the net to find the area of the two dimensional figure students will be able to connect this concept to three dimensional shapes. Also, students need to be able to recognize, describe and build simple 3-D shapes, including making nets for the shapes. For example: they can be shown or handed a cube or cuboid for the 3-D model and then given some squared paper on which to make a net that will make an identical shape. This involves using guided instruction to support the students as they develop the understanding of what shapes are needed for the faces in order to make the net and how it will all fit together. The students will also need to measure the sides of the given shape so that they know how long the lines on their net need to be. So, a net of a 3-D shape is what it looks like if it is opened out flat. A net can also be folded up to make three-dimensional shape. There may be several possible nets for one 3-D shape. It is important for students to recognize the attributes connected to the 3-D shape on the net. It is also important for students to understand how the net relates to the three-dimensional shape because when they start calculating the surface area they tend to get confused when they don’t understand that some faces on three dimensional shapes will have congruent dimensions.
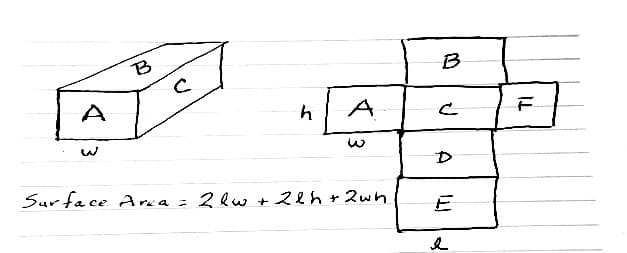
Once students have a good grasp on the concept of making a net for the 3-D shape the next step is for students to use the nets in finding the surface area of three-dimensional figures. To calculate the surface area of the object we need to find the area of each face and add them all together. For example, if we want the surface area of a cuboid or rectangular prism we would need to find the area of each face of the prism. Below is an illustration of a cuboid and its net. As you can see the area of Face A is product of w and h, Face B is the product of l and w, and Face C is the product of l and h. Since this is a cuboid we know the opposite face of A is F, then Face F will have the same area, the opposite face of B is D, then Face D has the same area as B, and the opposite of Face C is E, then E has the same area as C, and the last step is to add all the areas together. Hence the formula for the surface area of this cuboid is
SA=2lw + 2lh + 2wh.
This is shown in the following illustration.

Comments: