Transitions in the Conception of Number: From Whole Numbers to Rational Numbers to Algebra

Progressive problem set

For this unit, I have written a collection of problems that progress from very simple to more complex problems that contain a variety of operations with fractions.

Problems on fraction notation.

Problem I.

1) Write down a fraction that represents the area of the shaded region on the diagram above, compared with the whole diagram. Reduce the fraction to the lowest terms.

2) Write down a fraction that represents the area of the shaded region on the diagram below, compared with the whole diagram. Reduce the fraction to the lowest terms.

Problem II. ⁷

Use the diagram below to answer the following questions:

1) What fractional part of quadrilateral ABCO is triangle ABO?

2) What fractional part of quadrilateral ABCD is triangle ABO?

3) What fractional part of quadrilateral ABCD is quadrilateral ABCO?

4) What fractional part of hexagon ABCDEK is quadrilateral ABCO? Express this fraction in lowest terms.

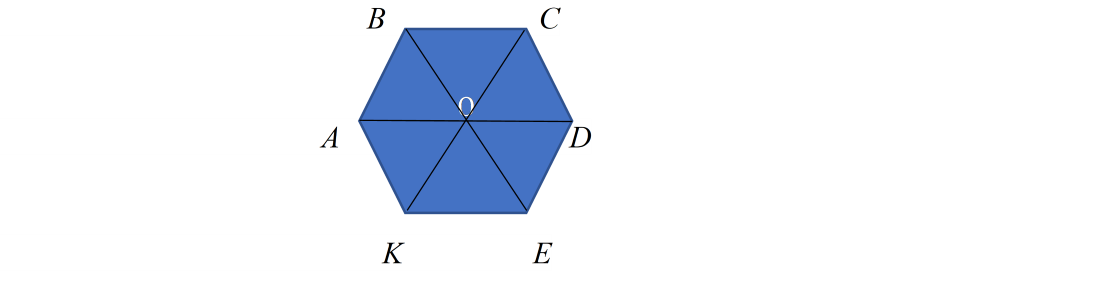
In Problem II 4), I ask students to reduce the answer to the lowest terms, because I think teachers should use every opportunity to have students practice on reducing the fractions.

Problem III.

1) What part of the (standard calendar) year is 1 day?

2) What part of the week is 1 day?

Problem IV.

1) What part of an hour is 45 min, 12 min, 15 min, 40 min, 35 min? Write down each answer as a fraction. Reduce the fraction to the lowest terms.

2) What part of a straight angle is 30⁰, 45⁰, 60⁰, 90⁰, 120⁰, 135⁰, 150⁰? Write down each answer as a fraction. Reduce the fraction to the lowest terms.

In Problem IV 1) students should understand that first they need to convert 1 hour into 60 min. In Problem IV 2) they need to know that the measure of a straight angle is 180⁰.

Problem V.

There is a 5-liter jar. Mrs. Brown poured a liters of water into the jar. What part of the jar is filled with water if a = 1, 2, 3, 4? What part of the jar remains empty?

In Problem V first, students should be able to plug in the given numbers for a and represent their answers in fraction notation. To answer the second question, then they should subtract these fractions from 1.

Problems involving a number line.

Problem VI.

1) On graph paper draw a number line. Let the unit length be equal to 5 squares. Put the following numbers on this number line:

¹⁄₅, ²⁄₅, ³⁄₅, ⁴⁄₅, ⁵⁄₅

2)  On graph paper draw a number line. Put the following numbers on this number line:

¹⁄₈, ³⁄₈, ⁵⁄₈, ⁷⁄₈

In Problem VI 1) students have a prompt regarding the scale of the number line. In Problem VI 2) this prompt is missing, and students are invited to figure out the best way to put the fractions on the number line based on their experience with Problem I 1). I also like to use this problem to reinforce the concept that if two proper fractions have the same denominator, the smaller fraction is closer to 0, while the bigger fraction is closer to 1.

Problem VII.

1) Without drawing a number line, decide which of the two points lies to the left. Explain.

A (³⁄₇) or B (⁵⁄₇).

2) Without drawing a number line, decide which of the two points lies to the right. Explain.

C (¹¹⁄₁₃) or B (⁹⁄₁₃).

In Problem VII students are invited to practice on mental Math. They should “draw” a number line in their imagination and answer the question. Their explanation should also be based on the principle of comparing fractions with the same denominator by comparing their numerators.

Problem VIII.

1) Use a piece of graph paper. Draw a number line. Let the unit length be equal to 6 squares. Place the following numbers on the number line:

3 ¹⁄₃, 2 ⁵⁄₆, 2 ²⁄₃, 1 ¹⁄₂

2) 1) Use a piece of graph paper. Draw a number line. Place the following numbers on the number line:

1 ¹⁄₈, 2 ³⁄₄, 2 ⁵⁄₈, 3 ¹⁄₄

Similar to Problem VI, students are given a prompt in Problem VIII 1) regarding the unit length. In Problem VIII 2) they should choose the unit length by themselves.

Problem IX.

Find the coordinates of points M, N, K, P, and E on the number line below:

This problem has a reverse assignment. A number line is given. Students should be able to write down the coordinates of each point in the form of a fraction or a mixed number.

Problems involving comparing fractions.

Problem X.

Arrange the given fractions first in ascending order, and then in descending order:

⁷⁄₁₂, ¹⁄₁₂, ⁵⁄₁₂, ⁹⁄₁₂, ¹¹⁄₁₂, ⁴⁄₁₂

Problem XI.

1) List at least five fractions that are greater than ¹⁄₉

It is obvious that the answers to Problem XI 1) will vary.

2)  List at least three fractions that are less than ⁵⁄₆.

3) List at least four fractions that are less than ¹⁄₂.

In Problem XI 3) students often represent ¹⁄₂ as a fraction with a larger denominator. For example, ⁵⁄₁₀. Then, their answer contains the list of fractions with number 10 in the denominator and numbers 1, 2, 3, and 4 in the numerator. Though this solution is correct, I will use the discussion of this problem to reinforce their understanding of the fact that all fractions with number 1 in the numerator and any natural number greater than 2 in the denominator will also be a solution to the problem.  

Problem XII.

1) Find all natural number values of x such that fraction ^x⁄₇ will be less than 1; equal to 1.

2) Find all natural number values of x such that fraction ⁸⁄_xwill be greater than 1; equal to 1.

3) What natural numbers can be plugged in for x to make a true compound inequality: ⁷⁄₁₃ > ^x⁄₁₃ > ⁴⁄₁₃?

Changing denominator of a fraction.

Problem XIII.

Find equal pairs of numbers in this set of fractions:

¹⁄₃, 1, ³⁄₆, ⁴⁄₁₂, ¹⁰⁄₂₅, ¹⁄₂, ³⁄₉, ⁷⁄₇, ¹⁰⁄₃₀, ¹¹⁄₁₁.

To answer the question students will have to reduce some of these fractions to the lowest terms to find equal fractions. They also should know that a fraction is equal to 1 if its numerator and denominator are represented by the same number.

Problem XIV.

The following points are marked on a number line:

A (²⁄₈), B (¹⁄₇), C (¹⁄₄), D (²⁄₁₄), E (⁵⁄₂₀), K (¹⁰⁄₇₀).

How many distinct points are there?

Problem XIV builds on Problem XIII. Students are not required to draw a number line in this problem. They should be able to find the same coordinates represented by equal fractions and draw a conclusion that equal fractions correspond to the same point on the number line.

Problem XV.

Prove the following inequalities:

1)

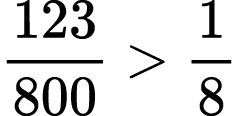
2)

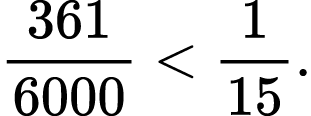
Problem XVI.

For what value of x is the equality true?

1)

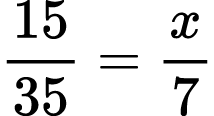
2)

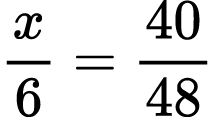
3)

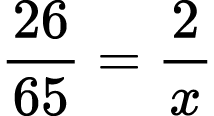
4)

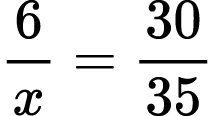
To solve Problems XV and XVI, students should reverse their plan of action and represent fractions with the smaller denominator as fractions with the bigger denominator. They could also put the given fraction in lowest terms.

Problem XVII.

Arrange the following numbers in ascending order.

1) ⁴⁄₅, ⁷⁄₁₀, ⁸⁄₁₅, ¹¹⁄₃₀

2) ¹¹⁄₁₂, ⁵⁄₂₄, ⁵⁄₆, ³⁄₈

In Problem XVII 1) and 2) it is pretty easy to identify a common denominator, and then represent all the members of the sets as fractions with the selected denominator and rearrange them in the required order. This question can be posed using descending order as well.

Now that students have practiced changing denominators of fractions, it is time to practice adding and subtracting fractions with different denominators.

Problems on adding and subtracting fractions.

In the beginning students should practice on fractions with the same denominators. In my experience, most students add and subtract fractions with the same denominators correctly. They understand these operations pretty well and feel comfortable. I would also use this opportunity to reinforce the usage of the Associative Rule of addition. This rule will let students save time and effort when calculating expressions with fractions. Students are given very little time to complete their tests. It adds to their stress and anxiety. A lot of problems they should complete without use of a calculator; and unfortunately, they are not used to it. First, let`s review the rule.

Associative Rule of addition:

If a, b, and c are any real numbers, then (a + b) + c = a + (b+ c).

Problem XVIII.

Find the value of the expression

1) ⁴⁄₁₁ + a, if a = ¹⁄₁₁, ³⁄₁₁, ⁵⁄₁₁

2) b - ¹⁄₁₀, if b = ⁷⁄₁₀, ⁵⁄₁₀, ³⁄₁₀

3) ³⁄₁₄ + (⁶⁄₁₄ + c), if c = ¹⁄₁₄, ²⁄₁₄, ⁵⁄₁₄

4) ¹²⁄₁₇ - ³⁄₁₇ - d, if d = ⁴⁄₁₇, ⁵⁄₁₇

In Problem XVIII 3) first of all, students should apply the associative rule of addition to add ³⁄₁₄ and ⁶⁄₁₄ .And in Problem XVIII 4) first, students should combine like terms, and only after that plug in for the variable. I will always encourage my students to reduce the answer to the lowest terms (sometimes it is already in lowest terms, so no work is necessary, except to check to be sure.)

Problem XIX.

Solve the equations:

1) ¹⁷⁄₂₀ - x = ¹⁴⁄₂₀ - ³⁄₂₀

2) ⁸⁄₁₅ - ⁷⁄₁₅ + y = ¹⁴⁄₁₅

3) ¹²⁄₁₉ - (¹⁄₁₉ + x) = ⁵⁄₁₉

4) ¹⁶⁄₂₇ + ²⁄₂₇ - y = ¹⁄₂₇

To challenge students even more, I ask them to solve these equations in their mind.  The first student who receives the correct answer should explain the steps he/she takes to do the mental Math. This small competition helps me train students to calculate as fast as they can to get them ready for a real-life task when students take tests under severe time pressure.  

Also, it is a good time to reinforce word problems. I am an absolute advocate of creating problem sets that ask students to practice on multiple concepts, especially on word problems since they have direct connection to the real world and develop students` critical thinking in the best way. So, the suggested problems may look like these ones:

Problem XX.

To make 8 pairs of pants a seamstress used 4 yds of fabric. To make 8 skirts she used 3 yds of fabric.

• How much fabric did she use to make a skirt?
• How much fabric did she use to make a pair of pants?
• Did she use more fabric to make a skirt or a pair of pants?
• How much fabric did she use to make a skirt and a pair of pants?

In a problem like this many student are tempted to divide 8 by 4 since it looks way easier and more attractive. Another surprising pitfall is linguistic. Not all of them understand that “a skirt” means “one skirt”. My Geometry students have made such a mistake many times. So, over the years I have developed a habit to make sure that the reading comprehension lets them move forward with this problem in the right direction. Finally, some students do not know that the sign of division can be replaced by a fraction bar. I make a point to review this with students before they attempt Problem XX. For example,

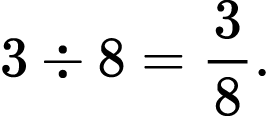
Problem XXI.

A farmer has 11 greenhouses of the same size. Tomatoes have been planted in 4 of them and cucumbers in 2 of them. What part of the greenhouses are occupied by tomatoes?

1. What part of the greenhouses are occupied by cucumbers?
2. What part of the greenhouses remain unplanted?

To solve this problem, students need to realize that the total number of the greenhouses should be in the denominator of the fraction.

Problem XXII.

A farmer has planted ¹¹⁄₁₇ of his fields with potatoes. Cucumbers occupy by ¹⁄₁₇ of the fields more than carrots, but by ⁸⁄₁₇ less of the fields than potatoes.

1. What fraction of his fields are planted with cucumbers?
2. What fraction of his fields are planted with carrots?
3. What fraction of his fields are planted with potatoes, carrots and cucumbers together?
4. What fraction of his fields remain unplanted?

Next come comparing, adding and subtracting fractions with different denominators. We should start with some simple problems and gradually increase the challenge.

Problem XXIII.

Find the value of each arithmetic expression. Put your answer in the lowest terms:

1)

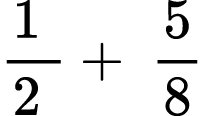
2)

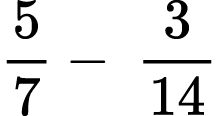
3)

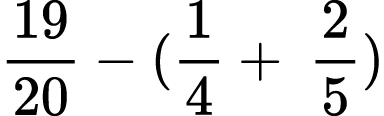
4)

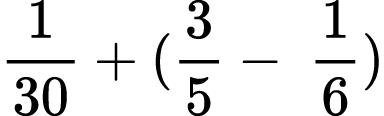
5)

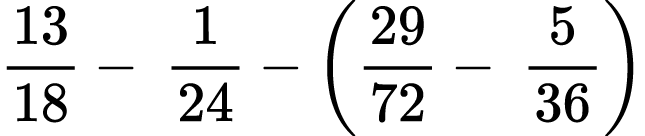
6)

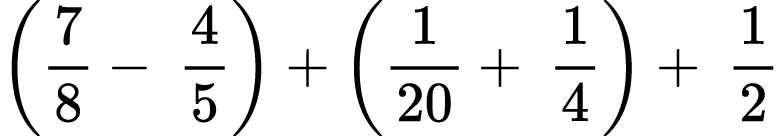
7)

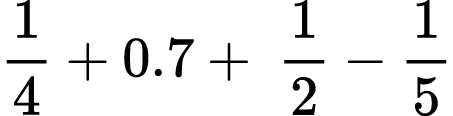
8)

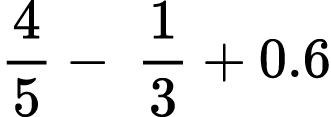
In Problem XXIII 7) and 8) students should replace decimals by fractions to solve the problem.

Problem XXIV.

Solve the equation:

1)

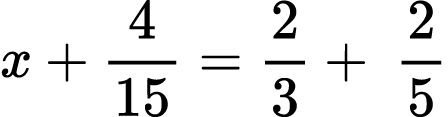
2)

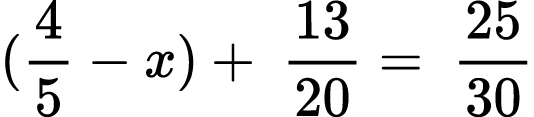
3)

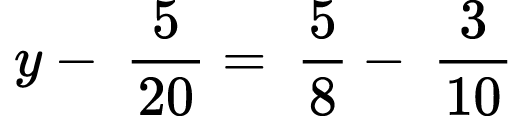
4)

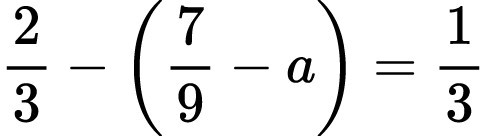
Problem XXV.

Find the value of each algebraic expression:

1) ^a⁄₁₀ + ^a⁄₁₅, if a = 1, 2, 5, 7

2) ^x⁄₁₂ - ¹⁄_x, of x = 4, 5, 6

Problem XXVI.

Points A (¹⁄_n) and B (¹⁄_m) are given on the number line below. On the same number line, label the following points:

1)

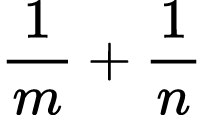
2)

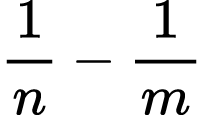
To solve these problems students can use a compass. They need to understand the principle of adding and subtracting numbers using a number line.

Word problems also come handy in teaching this concept.

Problem XXVII.

John played soccer for ⁹⁄₁₀ of an hour. Then he played volleyball for ⁹⁄₁₅ of an hour.

1. What game did he spend more time on?
2. How much time did he spend playing both games?

Problem XXVIII.

The length of a rectangle is ³⁄₄m, the width is less than the length by ⁵⁄₈m.

1. Find the width of the rectangle.
2. Find the perimeter of the rectangle.

Problem XXIX.

The first harvester can harvest an entire field in 6 days, the other harvester in 4 days.

1. What portion of the field can the two harvesters harvest in one day?
2. What portion of the field will remain unharvested after one day of work by both harvesters?

It is helpful to remind the students that the whole work on harvesting the field will be considered equal to 1.

Problem XXX

There are two motors of the same size. Each motor has its own tank. One motor consumes a full tank of gasoline in 18 hours, the other in 12 hours. What portion of the full tank will be consumed by both motors if the first will be working for 5 hours, and the other – for 7 hours?

Problem XXXI.

Jessica spent ¹⁄₃ of an hour reading the first book. She spent ¹⁄₆ of an hour more on reading the second book than on reading the first book. To read the third book she spent ⁷⁄₁₂ of an hour less than she spent on reading the first and the second book together. How much time did Jessica spend to read all three books?  Problems on multiplying and dividing fractions.

Problem XXXII

Find the product:

1)

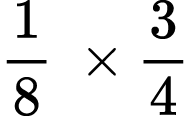
2)

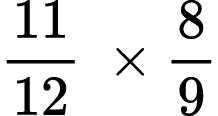
3)

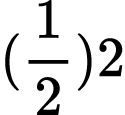
4)

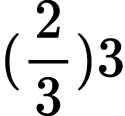
5)

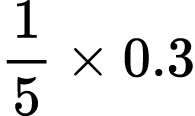
6)

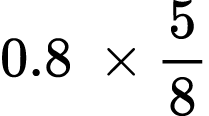
7)

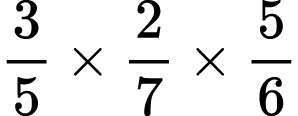
8)

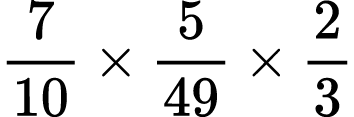
9)

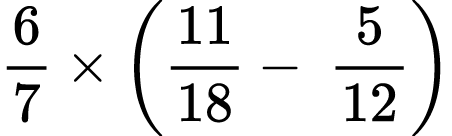
10)

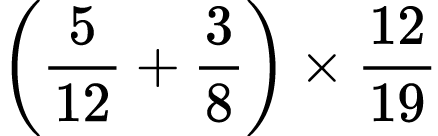
11)

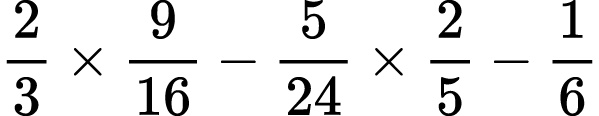
12)

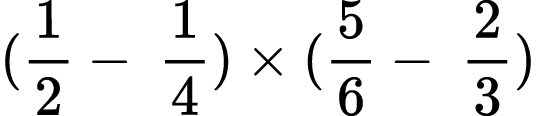
Problem XXXIII.

The mass of 1 liter of kerosene is ⁴⁄₅ kg. Find the mass of ³⁄₄ liter of kerosene, ¹⁄₂ liter of kerosene, ²⁄₅ liter of kerosene.

Note: It is extremely important to teach that to find a fraction of a number we should multiply this number by the fraction. So, in this case students should multiply ⁴⁄₅ by ³⁄₄, and so on. This skill becomes absolutely essential in algebraic expressions when students should find, for example, ²⁄₃ of x. They should be able to write it down as ²⁄₃X x

Problem XXXIV.

The length of a side of a square is ⁷⁄₈ in. Find the area of the square.

Note: I prefer that students write down a geometric formula first, and then plug in the number. A = s², so A = (⁷⁄₈)² in².

I will insist that they always specify the units in any measurement problem or word problem.

Problem XXXV.

Find the volume of a cube with a side length equal ³⁄₄ in.

This problem should be done in the same way as the previous one.

Problem XXXVI.

The velocity of a car is ³⁄₄km/min. Find the distance the car has travelled in ²⁄₃ min, in ¹⁄₆ min. Express the velocity in km/hr. Have you ever been in a car going that fast?

Problem XXXVII.

Find the quotient:

1)

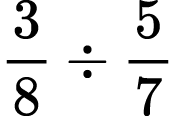
2)

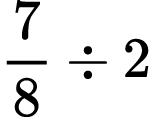
3)

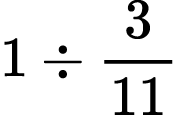
4)

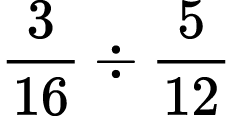
5)

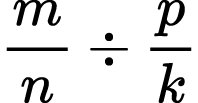
6)

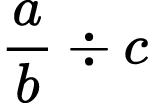
7)

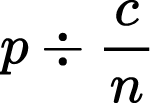
Problem XXXVIII.

The area of a rectangle is ¹⁵⁄₆₄ sq m. Find the perimeter of the rectangle if its width is ³⁄₈ m.

Problem XXXIX.

The length and the width of a rectangle are equal to ³⁄₄ in and ¹⁄₆ in respectively. Find the length of another rectangle, if its width is equal to ¹⁄₂ in, and the area is equal to the area of the first rectangle.

Problem XL.

The mass of ⁴⁄₅ cu dm of pine wood is equal to ²⁄₅kg.

• What is the mass of 1 cu dm of pine wood?
• What is the volume of the pine wood bar if its mass is equal to 1 kg?

Problem XLI.

Find the velocity of a vehicle if it travelled 15 mi in ⁵⁄₆ hour; in ⁵⁄₃ hour.