Evolutionary Medicine

Fundamental Concepts

Evolutionary Medicine: Evolutionary medicine is an interdisciplinary field that applies principles of evolutionary biology to understand health and disease. It examines how evolutionary processes, such as natural selection, genetic drift, and gene-culture coevolution, influence the prevalence of diseases and health conditions in human populations. By studying the evolutionary history of traits like lactose tolerance, scientists can gain insights into the genetic adaptations that have occurred in response to dietary and environmental changes over thousands of years (Gluckman, Beedle, and Hanson 2009, 102).

Mutation: Mutation refers to changes in the DNA sequence of an organism's genome. These changes can occur naturally due to uncorrected mistakes in DNA replication or external factors such as radiation or chemicals that can induce them. Mutations are a population's primary source of genetic variation, providing the raw material for evolution. Some mutations may be neutral, while others can be beneficial or harmful (Hartwell et al. 2018, 233). It is important to note that, in general, mutations are not beneficial, which could be why evolution is not a smooth, continuous process; it only happens in the population genetics occasionally when there are sudden jumps in genetic variations. These jumps may be attributable to the appearance of a beneficial mutation that increases an individual's fitness, allowing them to survive and reproduce more effectively, thus spreading the mutation through the population over generations.

Selection: Selection, or natural selection, is the process by which certain traits become more common in a population due to their beneficial effect on the survival and reproduction of individuals. Traits that confer a selective advantage increase frequency over generations, while disadvantageous traits become less common. Selection drives the adaptation of populations to their environments and is a fundamental mechanism of evolution. For instance, in populations where dairy farming was prevalent, individuals with lactase persistence had a nutritional advantage, leading to increased reproductive success and the spread of this trait (Futuyma and Kirkpatrick 2017, 45).

Genetic Variation: Genetic variation refers to the diversity of gene frequencies within a population. It arises from mutations, genetic recombination during sexual reproduction, and gene flow between populations. Genetic variation is crucial for the adaptability and resilience of populations because it provides a pool of traits that enable selection by changing environments. High genetic variation allows populations to adapt to new selective pressures, such as changes in diet or environment. For example, the variation in lactase persistence among different human populations illustrates how genetic diversity enables adaptation to various cultural and environmental contexts (Hedrick 2011, 56).Understanding these fundamental concepts of evolutionary medicine and their influence on population genetics can help students and teachers better appreciate the dynamics of genetic traits like lactose tolerance. Notably, the interdisciplinary approach for this unit not only reinforces algebraic concepts but also highlights the importance of mathematics in scientific research and real-world problem-solving.

Allele: An allele is a variant form of a gene, a DNA segment that codes for specific traits. Each gene can have multiple versions or alleles, resulting in different physical traits or characteristics. For example, in lactose tolerance, there are different alleles of the gene responsible for lactase production, the enzyme needed to digest lactose.

• One allele may code for the ability to produce lactase throughout adulthood (lactose tolerance).
• Another allele may code for reduced or no lactase production after infancy (lactose intolerance).

Individuals inherit their alleles from their parents, typically receiving one allele from each parent for each gene. Combining these alleles determines an individual's specific traits related to that gene. In population genetics, the frequency and distribution of alleles can provide insights into evolutionary processes, such as natural selection and genetic drift.

Allele Frequency: Allele frequency, also known as gene frequency, refers to how common a particular allele is in a population. We can express the allene frequency as a proportion or percentage of all the alleles for a specific gene in the population, which gives insight into the genetic diversity of a population and how that diversity changes over time due to evolutionary processes like natural selection, genetic drift, mutation, and gene flow. The following are critical points about allele frequency:

• Calculation: Allele frequency is calculated by counting how many times an allele appears in the population and dividing by the total number of alleles for that gene. For example, if a gene has two alleles, L and l, and in a population of 100 individuals, there are 60 L and 40 l alleles, the frequency of L(p) is 0.6, and the frequency of l(q) is 0.4.

• Hardy-Weinberg Equilibrium: In a population that is not evolving, allele frequencies remain constant from generation to generation, a state described by the Hardy-Weinberg equilibrium (Hedrick 2011). This principle provides a baseline (or null model) for detecting evolutionary changes.

• Evolutionary Processes: Changes in allele frequencies over time indicate that evolutionary processes are at work. For example, if the lactose tolerance (L) allele becomes more common in a population over generations, it suggests that lactose tolerance is being selected.

In this unit on lactose tolerance, tracking allele frequencies allows students to mathematically model how the trait for lactose tolerance spreads in different populations and understand the evolutionary forces driving these changes.

Genetic Drift: Genetic drift is a mechanism of evolution that refers to random changes in the frequency of alleles within a population's gene pool over time. Unlike natural selection, driven by differential reproductive success based on advantageous traits, genetic drift occurs by chance. This process can significantly impact small populations, where random events can lead to significant changes in allele frequencies from one generation to the next. The following are critical points about genetic drift:

• Randomness: Genetic drift is purely random. Events such as natural disasters, accidents, or random mating patterns can cause specific alleles to become more or less common, independent of their effect on survival or reproduction.

• Population Size: The effects of genetic drift are more pronounced in small populations. In larger populations, random allele frequency fluctuations tend to average over time.

• Bottleneck Effect: A population bottleneck occurs when a population's size is significantly reduced for at least one generation, leading to a loss of genetic diversity and making genetic drift more impactful.

• Founder Effect: When a new population is established by a small number of individuals from a larger population, the new population's allele frequencies may differ significantly from the original population due to the limited genetic diversity of the founders.

In this unit on lactose tolerance, genetic drift can help explain why specific alleles related to lactose digestion may become common or rare in isolated populations, regardless of whether those alleles confer a selective advantage.

Selection Coefficient (s): The selection coefficient (s) quantifies the relative fitness difference between genotypes in population genetics. Precisely, it measures the extent to which a particular allele or genotype reduces or increases the reproductive success of an individual carrying it compared to the optimal genotype in the population.

When studying lactose tolerance, the selection coefficient can help explain how genetic traits influencing lactose digestion are favored or disfavored in different populations. For example:

• A positive selection coefficient (s > 0) indicates that lactose tolerance provides a reproductive advantage, perhaps because individuals who digest lactose have better nutrition and health, leading to more offspring.
• A negative selection coefficient (s < 0) suggests that lactose intolerance might be disadvantageous in environments where dairy consumption is essential for nutrition.

Mutation Rate: The mutation rate is the frequency at which new mutations occur in a genome over a specific period, such as per generation or nucleotide per generation. Mutations are changes in the DNA sequence that can introduce new genetic variations within a population. These changes can occur due to errors during DNA replication, environmental factors, or exposure to certain chemicals or radiation. The following are critical points about the mutation rate:

• Measurement: The mutation rate is typically the number of mutations per gene, cell division, or generation. For example, a mutation rate of 1 in 1,000,000 per generation means that one mutation occurs in every million gene copies each generation.

• Impact on Evolution: Mutations are the ultimate source of genetic diversity, providing the raw material for evolution. Even though mutations have little or no immediate effect on fitness (most mutations are deleterious) (Ohta 1992, 263), they can accumulate over time and lead to significant evolutionary changes.

• Lactose Tolerance Example: In the context of lactose tolerance, a mutation in the regulatory region of the LCT gene (which encodes lactase) allows for continued lactase production into adulthood. The mutation rate for this specific change can influence how quickly lactose tolerance spreads in a population.

In this unit on algebra and lactose tolerance, understanding the mutation rate helps students appreciate how new genetic variations arise and how these variations can contribute to the adaptation and evolution of populations over time.

Linear Selection Models: In some cases, the effect of natural selection on allele frequencies can be approximated linearly over short periods if the selection coefficient (s) is small (meaning that the allele has only a slight advantage or disadvantage). The allele's frequency (L) is not close to 0 or 1 (where 0 means the allele is absent, and 1 means it is the only allele present in the population).

In these circumstances, the change in frequency of a beneficial allele in a population can be modeled using a linear equation, making it easier to predict how the allele will spread over time. This approximation is handy in educational settings, as it simplifies complex biological processes into manageable mathematical models that students can analyze using algebraic techniques. Students can explore the dynamics of evolutionary change quantifiable by understanding and applying linear selection models, reinforcing their algebra skills and deepening their understanding of population genetics.

The exponential model in the context of allele frequency variation due to selection is given by the equation (Hartl and Clark 2007, 89):

L(t) = L₀ ⋅ e^s⋅t

Where L₀ is the initial frequency, s is the selection coefficient, t is the number of generations, and L(t) is the frequency after t generations. For small s and, thus, small s⋅t, we can use the first-order approximation of the exponential function, e^s⋅t ≈ 1 + s⋅t,  as shown in Figure 1.

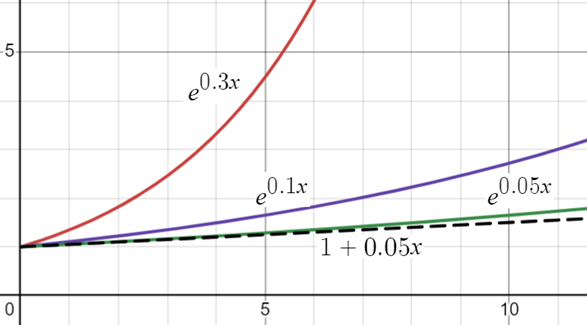
Figure 1. Graph of the exponential e^s•t model for s values of 0.3, 0.1, and 0.04 for the red, purple, and green curves, respectively. The dotted black line shows the approximate linear model 1 + st for s = 0.05.

Therefore, for small s, we can write:

L(t) = L₀ (1 + s•t), and

L(t) = L₀ + (L₀•s) • t, from where we get the linear Equation 1:

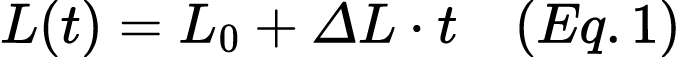
Where ΔL the frequency change L₀•s.

Following is an example. Imagine a beneficial allele A with a small selection coefficient s = 0.01. If the current frequency of allele A in the population is L₀ = 0.20 (20%), the frequency L(t), after t generations given by Equation 1 is:

L₀ = 0.20

s = 0.01

t = 1

Thus, after 1 generation, t = 1, the new frequency is:

L(1)= 0.20 + ( 0.20 • 0.01)•1 = 0.202 = (20.2 %)

This means that, under these conditions, the frequency of allele A would increase by 0.2% in the next generation. This linear approximation simplifies the prediction process, allowing scientists to estimate allele frequency changes due to natural selection quickly. Notably, Algebra in High School, mainly using linear models, provides powerful tools for analyzing and interpreting data in population genetics. Linear models can help students understand the relationships between different variables, such as the frequency of lactose tolerance in a population and various genetic and environmental factors. Students can apply linear equations to explore how these variables interact and predict future trends. This approach not only reinforces algebraic concepts but also highlights the importance of mathematics in scientific research and real-world problem-solving.

Multidisciplinary Teaching: This unit's integration of algebra with evolutionary medicine exemplifies the need for multidisciplinary teaching. By combining mathematical analysis with biological concepts, students can see the interconnectedness of different fields of study. This approach makes learning more engaging and helps students improve their performance in mathematics and science. The interdisciplinary nature of this unit aligns with educational standards and prepares students for Science Standards of Learning (SOLs) assessments by fostering critical thinking, problem-solving, and analytical skills.

By the end of this unit, students will improve their algebra skills and develop a deeper appreciation for the role of mathematics in understanding and solving real-world biological problems.