Dimensional Analysis Calculation Demonstrating Heart Reliability
The heart is a remarkable organ, which makes building a replacement for one an extremely daunting task. Unlike my car that I can stop, turn off, and park in the garage ready to use tomorrow, if my heart stopped beating for the night, I'd be in the morgue. The heart is so reliable that, frankly, I don't think about it most of the time. When my 98 year old grandfather died, his heart finally stopped, yet through his entire life, his heart had functioned literally without missing a beat. Assuming that his heart produced an average of 70 beats per minute, I can see that this works out to about:
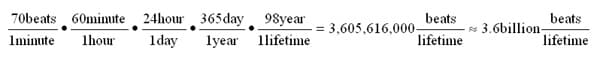
The calculation above illustrates the power of dimensional analysis, and demonstrates how easily I can make some incredibly surprising observations using fairly ordinary information. Dimensional analysis allows me to convert quantities to different units of measure that demonstrate or emphasize particular features of a system—in this case, reliability. Several things are going on simultaneously in the calculation, however, so I will break it down into more digestible pieces.
First, the calculation contains several fractions and the fractions contain units as well. I notice, in particular, that the unit of minute appears in the numerator of one fraction and the unit of minute appears in the denominator of another. These units can be rearranged to yield minute/minute. This fraction can be reduced: minute/minute =1. The result, 1, is now a number without units. I notice also that the equation has several examples of the same situation: hour/hour=1, day/day=1, year/year=1. In the end, the only units left in the calculation are beats/lifetime (beats per lifetime).
Fractions that compare a quantity of one type of unit with a quantity of a different unit are called rates. 5 I assumed that my granddad's heart rate was 70 beats/1 min for the purposes of my calculation. His rate of using his time on earth was 98 years/1 lifetime.
The other fractions in the calculation are a special type called conversion factors. In a conversion factor, the two units in the fraction measure the same type of thing. In the fraction 60 min/1 hr, both minutes and hours measure the same type of thing—time. In the conversion factor, the two quantities measure the same amount of the same thing using two different units. In other words, since 60 min = 1 hr, the fraction 60 min/1 hr really expresses the number 1. As learned in elementary school, when I multiply by the number 1, the value of the other number does not change. Although the value does not change, the number associated with the value and the units used to measure that value do change. Strangely, all of the fractions shown above—in which the numerator and denominator represent the same thing measured in different units—are also equal to 1. This concept can be a little confusing so I'm going to take a look at a simpler example.
A Clarifying Example
I own a yardstick. It is 1 yard long. I notice that the number here is 1 and the unit here is a yard. If I look at the foot measures on the yardstick, I see that it is also 3 feet long. In this interpretation, the number is 3 but the unit is feet. I have the same yardstick, and it's the same length, but if the units used to describe it change, the number associated with the units also changes. This demonstrates that 3 feet = 1 yard, and I can write the conversion factor 3 ft/1 yd, which I can use to convert yards to feet, or another conversion factor 1 yd/3 ft, which I can use to convert feet to yards. I could use my yardstick to make even more conversion factors by noting that the yardstick is also 36 inches long.

Comments: