Background Knowledge
The van Hiele’s Levels of Geometric Thought4
Level 0 – Visualization
Level 0 is the recognition of basic shapes based on how they look. As students begin to approach Level 1 they begin to understand classes of shapes. Students at this level can name basic shapes, but may be confused if the shape is oriented in a different way.
Level 1 – Analysis
At Level 1, the students start out with an understanding of the classes of shapes and move toward identifying the properties of shapes. Students at this level can recognize different representations of the shape, such as triangles that have 3 sides, but may appear different because of the lengths of the sides or the way the shape is oriented. In the analysis phase, students recognize and describe properties of the shape, such as a rectangle has two pairs of parallel sides, opposite sides have the same length, and there are four right angles. At Level 1 students may have difficulty understanding that all squares are rectangles or all rectangles are also parallelograms.
Level 2 – Informal Deduction
Students are able to think about the properties of the shapes and begin to see and develop relationships between these properties. Students may use if-then statements at Level 2. For example, if a shape is a rhombus with right angles then it is a square. At this level, students may understand that a shape may meet the definition with minimum characteristics. For example, if a parallelogram has one right angle, it is a rectangle. Or if a rhombus has one right angle, it is a square. At Level 2, students progress from understanding properties of shapes to understanding relationships among properties.
Level 3 – Deduction
At Level 3, the students begin to use a system to logically think about parameters that lead to the derivation of other truths. At this level, students are able to not only make conjectures, but also examine if they are true. This is the type of thinking that takes place in high school geometry. At the deduction level, students move from relationships among properties to deductive systems of properties.
Level 4 – Rigor
Students at Level 4 move from deductive systems of properties to analysis of deductive systems. This is typically the level of college math students focusing on geometry.
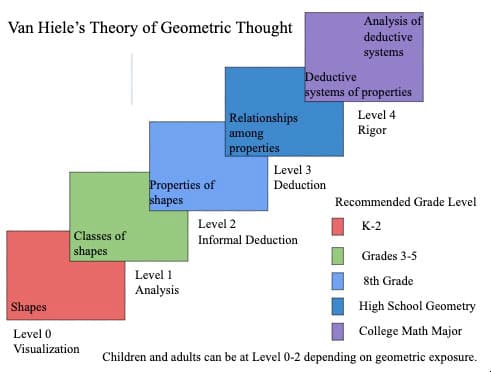
Figure 1: van Hiele’s Theory of Geometric Thought
The van Hiele’s Theory was developed in 1959. See Figure 1. This theory took a while to catch on in this country,5 but today it greatly impacts the American geometry curriculum.6
The van Hiele’s levels are sequential. The levels are not developmental but more experiential. “Geometric experience is the greatest single factor influencing advancement through the levels.”7 Some researchers believe a person can be at different levels depending on the specific topic and their exposure to that topic. Ideally, it is believed that the best way to help students advance through the levels is to instruct them on the students’ current level with explorations, interactions, and discussions at the next level. This is basically the same approach used with reading instruction. Students read on their independent level and are exposed to a higher level through read aloud or small group instruction with support. Just as with reading, if the level is too high, the students will have difficulty engaging with the material and will not have much to contribute to discussions.
Implications
According to Van de Walle & Lovin, “Nearly all students in K-3 will be at Level 0, by at least grade 3 teachers certainly want to begin to challenge students who seem able to engage in Level 1 thinking.”8 The expectation is that students will be at Level 2 by the eighth grade, Level 3 in high school geometry, and Level 4 as a college math major.
I will use the van Hiele levels throughout the curriculum unit to identify the level of each activity involving area, perimeter, and quadrilaterals. Suggestions for differentiation at a lower level as well as ways to move the activity to a higher level to meet the students’ needs will be made.

Comments: