Perimeter, Area, Volume, and All That: A Study of Measurement

Quadrilaterals

General quadrilaterals

Quadrilaterals are polygons with four sides. Many classes of special quadrilaterals have been singled out for study. Some are more general, and others are special and have specific properties.

Special Quadrilaterals

A trapezoid is a quadrilateral with at least one pair of parallel sides. Some people prefer to require a trapezoid to have only one pair of parallel sides, but “at least” is the definition we will use in this unit. See Figure 2.

A parallelogram is a quadrilateral with two pairs of parallel sides. This implies that opposite sides have the same length, and vice versa. A kite is a quadrilateral with two pairs of adjacent (next to), equal sides. A quadrilateral with four congruent sides is a rhombus. A rhombus is both a kite and a parallelogram. A rectangle is a quadrilateral with four right angles. A rectangle is a parallelogram. A rectangle that is also a rhombus is a square. The square is the most special of all quadrilaterals as it has many properties and lots of symmetry (see Table 1).

Properties of Quadrilaterals

Properties of Quadrilaterals

Table 1: The properties of quadrilaterals.

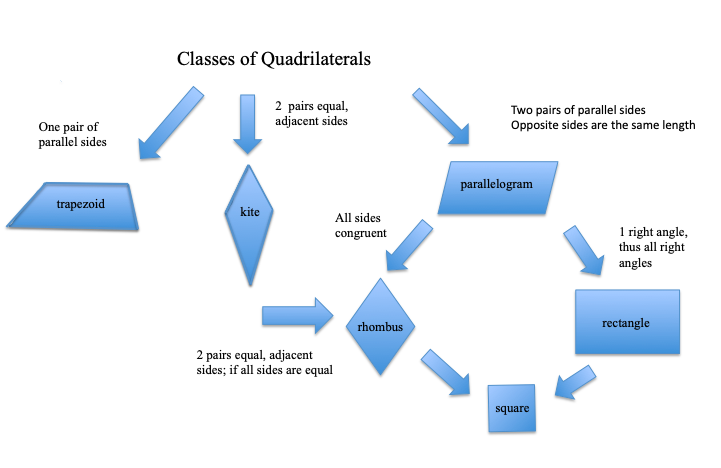
Figure 2: A diagram of special types of quadrilaterals

Symmetry

Symmetry can also be used to distinguish classes of quadrilaterals. Some have lines of symmetry, rotational symmetry, and reflection symmetry across a diagonal.

A shape has rotational symmetry if, when it is rotated, or turned, it appears to be in the same position. The only possibilities relevant for quadrilaterals are 90 or 180 degrees. A quadrilateral with 180-degree rotational symmetry is a parallelogram (and vice versa) (see Figure 3). The only kind of quadrilateral with 90-degree rotational symmetry is the square.

Figure 3: This shape has rotational symmetry because it will get back to the original position when rotated less than 360 degrees.

A shape has symmetry across a line (aka reflection symmetry) if, when it is folded across the line, the two halves match exactly (see Figure 4).

Figure 4: This figure (an isosceles trapezoid) has reflection symmetry. If the line of symmetry goes through a side, it will pass through two opposite parallel sides, and you have an isosceles trapezoid.

Reflection symmetry across a diagonal is when a figure is folded on a diagonal, and the two halves line up exactly (see Figure 5).

Figure 5: If the line of symmetry is a diagonal, you get a kite.

A diagonal of a quadrilateral separates it into two triangles. If the triangles are congruent, then the quadrilateral is a kite (if the halves are reflections of each other across the diagonal), or it is a parallelogram (if the halves are congruent by 180 degree rotation around the midpoint of the diagonal). If all four triangles are congruent when both diagonals are drawn, then the shape is a rhombus.

A rhombus is the only quadrilateral with reflection symmetry across both diagonals (see Figure 6).

Figure 6: A rhombus is a kite with all sides equal. A rhombus is symmetric across both its diagonals.

Figure 7: If the rhombus is folded along the diagonal line, the two triangles will lie on top of each other and will be aligned evenly.  A rhombus with right angles is a square.

By drawing the diagonals of quadrilaterals students can discover characteristics and relationships between the different classes (see Figure 7). Students can describe the characteristics that result from the two diagonals.

The diagonal forms two congruent triangles (see Figures 8 and 9).

Figure 8: In a parallelogram each diagonal forms two congruent triangles.

Figure 9: In a parallelogram, diagonals also bisect: each cuts the other into two line segments each of the same length.

Another characteristic of the diagonals (of parallelograms) is that the point of intersection of the diagonals is a central point, that bisects or splits each line segment into two segments of equal length (see Figure 9). Also the parallelogram is symmetric under 180- degree rotation around this point. Thus, although the typical parallelogram does not have any reflection symmetry, it does have 180-degree rotational symmetry, and this accounts for all the commonly stated properties of the parallelogram (opposite sides are equal and parallel, opposite angles are equal, diagonals bisect each other, etc.) (see Figure 10).

Figure 10: The parallelogram shows diagonals that bisect.

In a kite, diagonals intersect perpendicularly (see Figure 11). The diagonals can be perpendicular without bisecting each other. In fact, they can be perpendicular and equal without bisecting each other. In a kite, one of the diagonals will bisect the other one, but not necessarily vice versa. Diagonals that are perpendicular and bisect each other reveal that the shape is a rhombus.

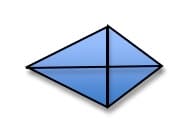
Figure 11: In a kite, the diagonals intersect at right angles.

An analysis of diagonals is another way to classify and explore relationships among quadrilaterals.

I have created a “tool” that my students will use to investigate the diagonals of quadrilaterals. I name the tool a “Crisscross Vise.” I tweaked a design with paper to turn it into more of a tool. I crafted it using two straws joined by a brass fastener. I punched equidistant holes in the straws (see Figure 12).

Figure 12: A crisscross vise made with straws and a brad fastener.

Then I searched on Google^® and discovered a real tool for construction called a Crisscross Vise. The “real” device was invented in the mid 19^th century and is used to maintain parallelism.⁹ The exploration of quadrilaterals using the Crisscross Vise is in the activity section of this unit.

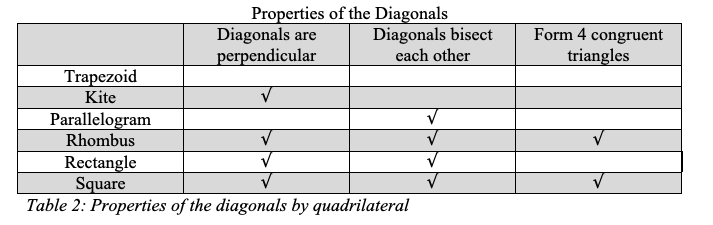
The diagonals of a rectangle do not form 4 congruent triangles. The pairs of opposite triangles are congruent, but the two pairs are not congruent, unless the rectangle is a square.

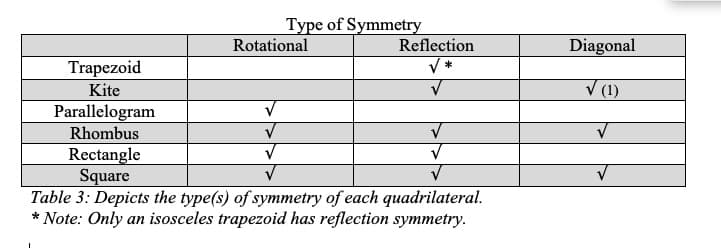
Earlier I stated that the square is the most special quadrilateral because of all of its properties and its symmetry. If you look back at the three tables, the square has checks in each column. The square has 10 out of 10 properties (see Tables 2 and 3). That shows clearly that the square is so special!