Sample Activities
Activity 1 – What is a Fraction
I will make sure to set the ground rules and procedures for modeling. When I am modeling all pencils and books should be down. All eyes are on me, the teacher. My students need to understand that they learn with their eyes and ears. During modeling, I have my students seated on the carpet. I am standing at the front of the class so that all the students are able to see. Once I am done modeling, I will circulate around the room to make sure that all students are on task and assist students who need help.
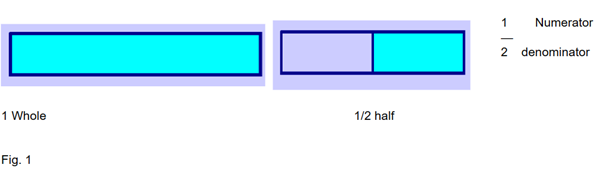
I will start the lesson by displaying my anchor chart with the definition of a fraction and ratio. Next, I tell the students that: A fraction is a ratio or number or part that describes the size of a given quantity in comparison to a unit of the same type. I will move on to tell the students that a ratio tells you how large a given quantity is in relation to a unit of the same kind. Here I have one sheet of paper. This sheet of paper is a shape. It is square. One whole sheet of paper can be divided into different fractional parts. I will hold up the paper for each student to see. I will fold the paper in half to show ½ of the paper. I will make sure to fold the paper evenly so that the parts are equal. A half is one of two equal parts. I will ask the students to notice that I folded the paper in half. If I cut the paper in half, I will have two halves. Now I put the two halves back together to make 1 whole sheet of paper. I will go to my anchor chart to show what 1 whole looks like. Once I have folded the two halves together, I will draw the corresponding figure. I will tell students this is what ½ looks like. I make sure to label ½ on the chart. Now I will introduce the vocabulary words numerator and denominator. I tell the students that the numerator is the top number of a fraction. The denominator is the bottom part of the fraction. It is the number of equal parts into which the whole has been divided.
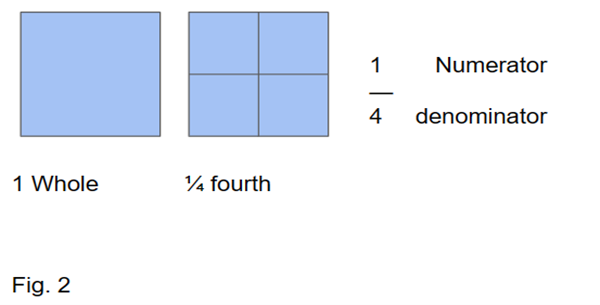
Next, I will fold 1 whole sheet of paper in half making sure that it is even. I will show the students that I have made halves. Now I am going to fold the paper once more. Now I have 4 equal parts. I will ask if I put the four parts together to make a whole like we did before? I will allow wait time so students can answer. Now that we know that we can piece the parts back together to make a whole. We can name the part of the fraction that we partition. There are four parts and the name for these fractional pieces is fourths or quarters.
Now we will try one together. If we take 1 whole sheet of paper and fold it evenly 3 times how many equal pieces would we have? What would we name those fractional parts? Could we piece those shares together to make a whole? I will ask two students to repeat the instructions to make sure all students know what the task is. I will give each student paper and have each student fold the paper 3 times, then unfold to see if they can get 8 equal pieces. Once students have completed the task they will turn and talk to a partner and discuss what their results were. I will call on 1 group to share their results. When students are sharing out all students should be focusing their eyes on the presenters. Students will explain step by step how they got their answers.
Once the selected students are done sharing, I will ask what the students have noticed about parts and wholes. I will ask a student to name the parts of fractions. For example: If I have a whole sheet of paper and fold it into four equal parts, what is the name for the four parts? The student should say fourths. If I have 6 equal parts what is the name for six parts? The student should say sixths. I will model folding the paper into sixths. Now that students have grasped the concept of what a fraction is and have learned to name the fraction, it is time to work independently on naming fractional parts.
Students will answer the following questions and label the parts of the fraction. What is the name for the following fractional part? Label the numerator as well as the denominator for each problem. Students should say sixth. They should go on to label the whole as the fraction as 6/6. This demonstrates mastery. I will go on to tell them that 6/6 is the same as 1 whole. If some students are having trouble, I will have them count each part and piece them back together. I will ask them how many parts they have counted. I will have students to piece the parts back together to make 1 whole.

Comments: