Addition and Subtraction of Fractions with Like Denominators
For illustrating addition and subtraction with the area and linear models, it is best if students are already familiar with doing that with whole numbers. Addition and subtraction of whole numbers and of fractions use the same principles. For the linear model, it is joining (for addition) or comparing (for subtraction) lengths. Then with fractions it is "just the same", except that you are combining multiples of a smaller unit. For the area model, it is pretty much the same as the linear model except that the shapes have some width. When using the area model with the addition of fractions, students must be reminded that each of the fractions to be added should be represented by its own region, disjoint from the other one. It is not so much having separate wholes, as the fact that you want to combine disjoint regions. For subtraction, you are "comparing" regions, which means you fit one inside the other, and find the part of the larger one that is outside the smaller one. Note that the original fractions that you want to add may be larger than 1. It is probably a good idea to do examples where this is the case. You are trying to put the parts together. The sum may be less than a whole or more than one whole.
When given the problem to illustrate and solve "two-sixths" plus "three-sixths", student will draw two rectangles (figure 19). They will then look for the unit being described. In this case it is sixths. Reminding students of the adjective-noun relationship would be a good idea to reinforce looking for the same unit. Since the student knows that both rational numbers are describing the same unit, one-sixths, then they can partition both rectangles. Substantial practice with adding rational numbers using the area model with the same unit is needed at this point. Students can see that the numerator is added but the denominator remains the same and can further reason we change the numerator because you are simply putting the pieces together. The unit will remain the same.
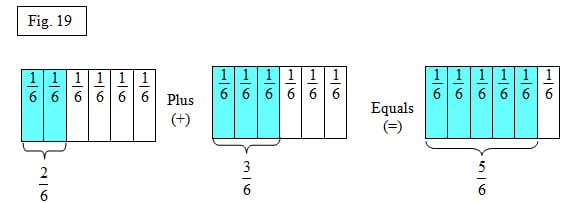
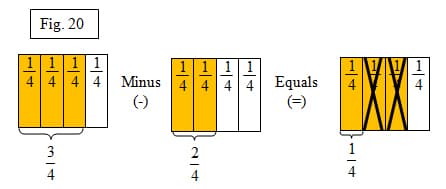
Subtraction of fractions will work the same way using the area model by simply taking away parts of the first area model. Figure 20 shows how to solve for "three-fourths" minus "two-fourths". Again, here we remind students that we are working with two separate wholes.
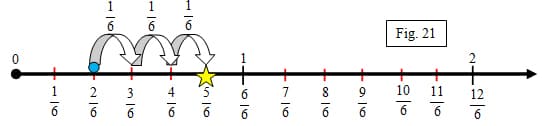
The linear model would further simplify the addition of fractions with like denominators. Just like with whole numbers on a number ray, students can move away a specified distance from the origin 0 and move towards a specified distance to the origin 0. Let's show the example from above on the number ray model. We will illustrate "two-sixths" plus "three-sixths"(figure 21). We know that "one-sixths" is being described, so therefore "one-sixths" is our unit we are working with. We should divide each section between the whole numbers in six parts. Since we are adding we can start with either fraction. When we subtract we will need to start with the "bigger" fraction. "Two-sixths" is two-sixths from the origin. Let's begin there. From "two-sixths" we will then travel three more times of the unit fraction "one-sixth". We "land" on "five-sixths".
We can do the same with the subtraction problem, "three-fourths" minus "two-fourths". We know that "one-fourths" is what is being described and therefore is our unit. We will divide each section between the whole numbers in "one-fourths". Just as subtraction with whole numbers begins with the larger number, so will fractions. It should be said that kids should have understood that if the units or denominators of two fractions are the same, then the numerator will be used to say which fraction is "more than" the other. Students can also locate those fractions on the number line to verify which fraction is "more than". Since "three-fourths" and "two-fourths" share the same unit, "one-fourth", we can look to how many "one-fourths" we have. We can say that we have three "one-fourths" and we have two "one-fourths". Since three is more than two, we can conclude that "three-fourths" is more than "two-fourths". We will need to locate "three-fourths" on our number ray first (figure 22).
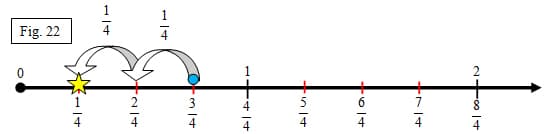
"Three-fourths" is three "one-fourths" from the origin. Since we are subtracting we will need to go backward to the point of origin, 0. We will travel two "one-fourths" back to the origin. We "land" on "one-fourth". For proficiency, students will need to continue practice of addition and subtraction of fractions with like denominators.

Comments: