Linear Model
In addition to the area models the use of the number line can contribute to the understanding of the fractions. 10 It is important that prior to working with the number line that students understand the concept of linear measurement. We are using the number line as a ruler to measure a distance from an origin. Students would also need to have this understanding of a number line. Teachers and students will use the number ray with the origin being 0.
Students can see that a number ray is very similar to a ruler (fig. 11). We assume at this point they have had some experience in using a ruler and we can then have them look at a ruler as if it were a number ray. I use rulers that only show inches in my classroom. Rulers that show centimeters can also work. This could be a good beginning for them to see what a number ray would look like when drawn.
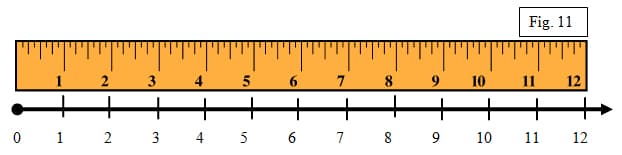
Many of my students are not able to draw and label a number line unless I give them practice. This will allow them to see the spacing between the numbers is also even. Students should be able to relate the above numbers to whole numbers and see that the ruler will have 12 whole numbers and that their number ray will also have 12 whole numbers (fig. 11). Now that they are familiar with drawing a number line, you can enlarge the pieces that you need (fig. 12). To focus on locating the unit fractions, I will enlarge the zero to two piece and use that to find the unit fractions for halves, thirds, fourths, fifths, sixths, sevenths, eighths, ninths, and tenths. The unit fractions will be found between the origin 0 to 1.
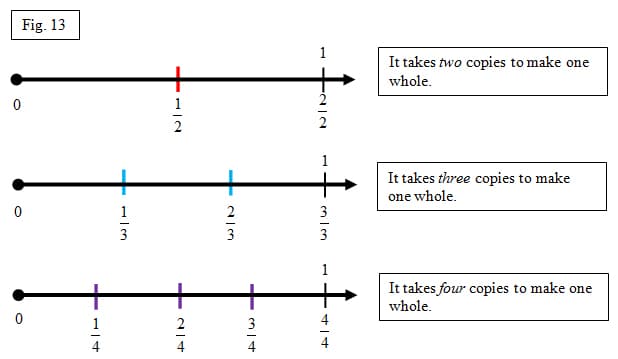
I want them to be able to notice on the number ray, what happens to the actual parts. It is important for students to understand the actual size of each of the unit fractions. Below in figure 13 are examples of halves, thirds, and fourths. The points are labeled according to their distance from the origin. Thus, two-fourths is twice as far from the origin as one-fourth; three-fourths is three times as far as one-fourth. Since it takes four one-fourths to make one, one is equal to four-fourths and is four times as far as one-fourth.
It is also important at this point to note to students they can continue to use the unit fraction to continue past the whole number one to divide the number ray. This will show that they can create any multiple of the unit fraction. They can then see that whole numbers are multiples of a unit fraction as well. Let's use "one-third" to illustrate. The whole number three is nine 1/3's from the origin (figure 14.a).
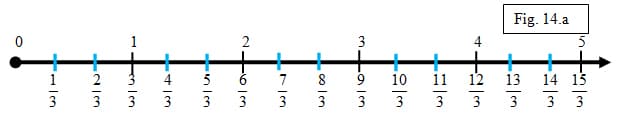
Once students are comfortable with representing fractions in area models and number line models, they should connect the fraction to division as well. The whole number 2 can be written in fraction form as six-thirds; but we also know that 6 divided by 3 equals
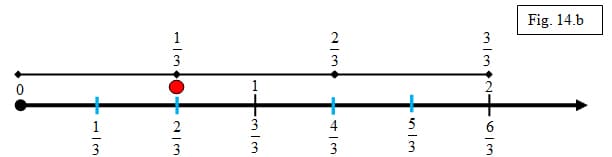
2. The whole number 3 can be written in fraction form as nine-thirds; and 3 is 9 divided by 3. The whole number 5 can be written in fraction form as fifteen-thirds; and 5 is 1/3 of 15, or 15 divided by 3. The number line supports that a fraction is linked to division by showing that it takes 6 copies of one-third to equal two, 9 copies of one-third to equal three, and 15 copies of one-third to equal five (figure 14.a). This extends to fractions as well. By subdividing the interval from 0 to 2 into 6 copies of 1/3, students can see that 2/3 is also equal to 1/3 of 2, or 2 divided by 3 (figure 14.b)
They can also connect this to multiplication. In the number ray displayed in figure 15, "four-thirds" is four of "one-third". If they multiply "one-third" by four they would have the general fraction "four-thirds".

Once students have an understanding of multiples of unit fractions on a number ray, then they will need to practice finding different general fractions on a number ray. This is key to connecting the number ray with arithmetic of fractions.

Comments: