Math Content
Rational Numbers
During the intensive session of the Yale National Initiative, I learned that a fraction is a name for a rational number. A fraction IS an actual number! My students would want to disagree with this idea. They would say that a fraction is made up of two numbers but is not really a number. I want to convince my students that a fraction is an actual number.
In the lower grades, students may have used the part-whole subconstruct to learn about and name fractions (fig. 1a and 1b). This subconstruct may help in just naming simple fractions of sets or groups.

However, once we move to more advanced concepts of rational numbers, this subconstruct could cause errors and create misconceptions (fig. 2). 5 One such misconception is that fractions should be added by adding the numerator and adding the denominator.
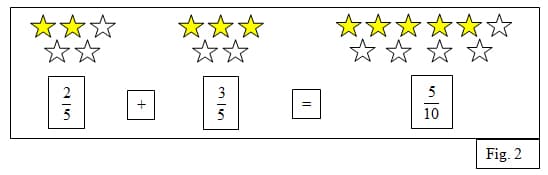
Of course this equation 2/5 plus 3/5 equals 5/10 is not correct. Students are using their understanding of basic addition properties to add the fractions. When we add we must be sure to have the same unit. However, in the example in figure 2 the student does not understand that the 2/5 is referring to a group of five stars, and 3/5 is referring to another group of five stars, but that the 5/10 is referring to a group of ten stars. The first two have the same unit, but the total sum is referring to a different unit. This goes back to the misconception of how my students view fractions made up of two numbers. The Part-Whole subconstruct may be ok in the lower grades to initially relate to fractions; however it does not assist with the more advanced concepts of rational numbers. Not only do we need to move away from this subconstruct, but students will also need to reconceptualize the meaning of a fraction. I will teach my students that a fraction is a number that describes a specific unit.

Comments: