Comparing Fractions with Unlike Denominators
Comparing fractions with unlike denominators can be difficult for some students. I suggest reading the section on equivalent fractions before attempting the comparison of fractions with unlike denominators. However if students are confident with the area model then they can master comparing fractions with unlike denominators. The number ray can also be used; however, for this unit I will only use the area model for comparison of fractions with unlike denominators. The technique that will be illustrated can be used to derive the cross multiplication algorithm, and provides a justification for that algorithm. Many people know the "trick" to cross multiply to compare fractions with unlike denominators. However it is not just a trick! There is reasoning behind why it works! Let's compare the fractions "two-thirds" and "three-fifths". They do not have the same unit, denominator, but we can still compare them. We know that we need to illustrate thirds and fifths. The area model will function like a multiplication array (figure 25). We will create an area model with thirds first. Shade the fraction that is being compared. In this case we will shade "two-thirds" in yellow. Using the same area model, we will then divide to show fifths. The equal horizontal strips are each 1/5 of the whole. We are again using repeated subdivision. 12 Essentially, it is creating an equivalent fraction. Once you have the area model divided in "one-fifths", shade the fraction being compared. I have shaded three-fifths in stripes.
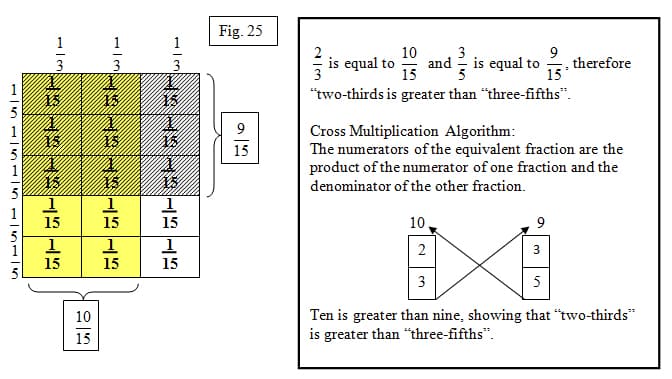
You have created an area model with fifteen equal parts. Each rectangle now represents "one-fifteenth" of the whole. Students can connect three multiplied by five equals fifteen with "one-third" multiplied by "one-fifth" equals "one-fifteenth". You can see that "ten-fifteenths" is equal to "two-thirds" and that "nine-fifteenths" is equal to "three-fifths". This area model in itself is the illustration of the cross multiplication algorithm we are so familiar with. The new numerators of the fractions are the products of the numerator of one fraction and the denominator of the other fraction. Now we can compare easily.

Comments: