Renaming Fractions
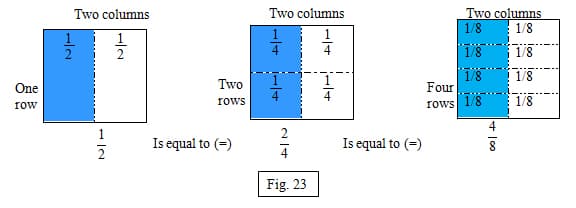
Many fractions can name the same number. For example, one-half names the same number as two-fourths, three-sixths, four-eighths, and even fifty- hundredths! Understanding repeated subdivision and reconstitution is a "key prerequisite" for understanding addition of fractions with different denominators. 11 Let's take a look at using the area model and repeated subdivision (figure 23). We know that "one-half" can stand for all those other fraction names, but how can we prove it? Subdivision basically says that you can partition an area model more finely to create a same name fraction. You can think back to a multiplication array. But also keep in mind that when you use subdivision, you are creating a new unit. In figure 23 the first area model displays 1 row and two columns. I now have two one-halves. The unit fraction is one-half. I will then divide the area model again in another half. The second area model is divided to show two columns and two rows. The area model displays four parts of the original whole, and students should be able to see that all the parts are equal. Therefore, I now have fourths; each small square is one-fourth of the whole. The one-half of the first area model is the same as two one-fourths of the second area model. In the third area model, I divide the same whole with four rows. This will give me eight equal parts and therefore giving me a new unit of one-eighths. The same one-half fraction is the same as four-eighths. Students should be able to notice that this idea of subdivision resembles an array of multiplication.
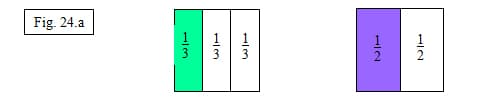
In understanding these rules, students then can rename any two fractions with unlike denominators to have the same denominator or unit. Using the area model can further ease renaming fractions with unlike denominators. Understanding of this strategy is key to adding and subtracting fractions with unlike denominators. For example, when given 1/3 and 1/2 we can use the area model to rename both fractions. We would first illustrate both fractions with its' own area model. Each model must be of equal size (figure 24.a).
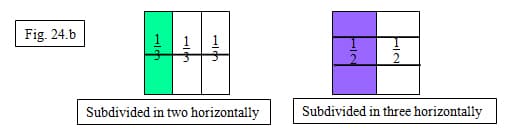
We use the denominator of the other fraction to subdivide the area model. We would subdivide 1/3 in two parts because two is the number in the denominator of 1/2. We would subdivide 1/2 into three parts because three is the denominator of 1/3. It is also important for students to know that they would subdivide in the "opposite" direction. In the example we originally showed both fractions with division of the area model vertically. We would then need to subdivide horizontally to rename the fraction. In figure 24.b, subdividing horizontally is the "opposite" direction. Students can show their original area model divided either horizontally or vertically, but must be sure to subdivide in the "opposite" direction.
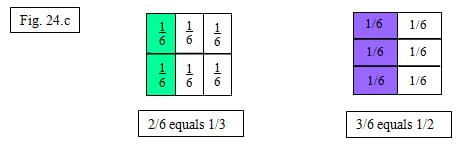
Students will see that each area model now has six parts. Using their knowledge of naming unit fractions, students will be able to recognize that a new unit of 1/6 was created (figure 24.c). They can then see how many multiples of 1/6 is equal to 1/3 and 1/2. We have renamed the fractions to share the same unit. Students should then reason that they can simply multiply the denominators to rename fractions.

Comments: