Concept #3: Comparing Integers on the Number Line
When working with number lines, my students will be able to see that these whole numbers inherently have order to them. They will see that the larger number will live to the right of the smaller number. This concept is rarely realized by my students because I have had to explain why -2 is greater than -3. The confusion arises from my students thinking about magnitude. Indeed the magnitude of -3 is greater than -2. I want to promote the idea that -2 is more positive that -3 and I have to be careful with the terminology that I use. Having students compare different types of pairs of numbers on the number line will help them visualize which number is more positive, or to the right. Once they have located these whole numbers, students will be able to place inequality signs between the pairs to formally order them. This activity will be approached in stages. First, students will compare sets of positive numbers.
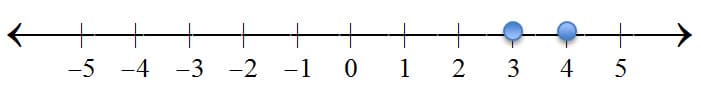
Figure 8
Figure 8 shows a number line with 3 and 4. Conclusion: 3 < 4. Students should interpret this as “4 is to the right of 3” or as being more positive. Next, students will compare one negative and one positive number.

Figure 9
Figure 9 shows a number line with -3 and 4. Conclusion: -3 < 4. Students should interpret this as “4 is to the right of -3.” This should cause no trouble, however in terms of magnitude, a more difficult problem would be -4 < 3. I will encourage my students to follow the progression of problems at attack them the same way. Placing or locating the integers first will help minimize errors in thinking. Last, I will have students compare two negative numbers.

Figure 10
Figure 10 shows a number line with -3 and -4. Conclusion: -3 > -4. Students should interpret this as “-3 is to the right of -4.”
The above-mentioned placement and comparison models are taught in 6th grade. However, they are still relevant to explore in this unit. This will help lay the foundation for operations in Aaron’s companion unit that mainly deals with addition and subtraction. Various numbers sets for comparison will be found in the appendix. A2

Comments: