Big Numbers, Small Numbers

Classroom Activities

To reinforce the content objectives presented, the students will complete several interactive activities in class. For me, these activities can serve as both informal and formal assessments. The activities can also be completed individually or in a small group. Based on my previous experience, I will have my students complete the first activity listed below in a small group format. I expect this to lend itself to a great deal of math talk which further promotes comprehension of the skill.

Toys R Math Activity

In this activity, the students will have the opportunity to shop from a teacher created toy store advertisement. The advertisement will be a combination of the most popular and not so popular toys that students in this age group enjoy. Students will use multiplication to finalize their purchases i.e. 2 Xbox One Controllers = $60 x 2 = $120 or 17 Zuru Fidget Cubes = 17 × $12 = $204. This activity can be differentiated to fit the abilities of the students. By specifying exactly how many of each toy a student must buy, the student can be supported with scaffolding. I will further allow the students to take a more open inquiry-based approach by giving them a specific budget and instructing them to see how close they can get without going over that budget. This approach provides enrichment for the students who need more of a challenge. This option forces the students to also review subtraction as they make their purchases. Once the students have finalized their purchases they must then write a check to cover the cost of their items. This seemingly small task allows the students to practice this realistic skill in a non-intimidating manner while simultaneously reviewing how to read, write, and identify numbers in both standard and word form. Writing the check also allows the students the opportunity to practice writing their signature, which seems to be a forgotten skill in this era. Once all groups have finalized their transactions, each group will then share with the whole class what they purchased and the method they used to generate a total.

If I want to extend this activity to include review standards, I could ask the students to order the total amount spent by different groups from least to greatest or vice versa. The students could also add the totals that each group obtained to comprise a class total which could then be compared amongst the three classes that I teach.

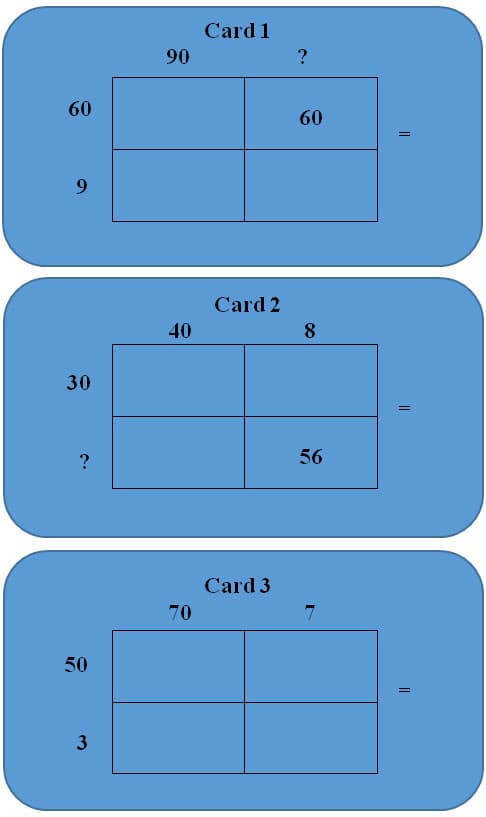
What’s Missing?

This activity is a scoot game. Scoot games are played with the whole class simultaneously in which the teacher will place a question card on each student’s desk. To play, students move around the room, from desk to desk, solving the math problems. As the students rotate around the class they will have to either complete what is missing from the grid model and then solve the problem or find the missing partial product that completes the Box Method. (Examples of game cards are shown below.) Since the students are moving around the classroom this will be an individual activity. To allow the students the opportunity for more math talk (Think-Pair-Share Strategy), they can work in pairs or small groups depending on spacing which will limit the number of scoot cards that are distributed on each desk.

This activity, like the previous one, can be differentiated. When looking at the three types of cards below one can easily see that there are different aspects of each algorithm missing or the card requires you to carry out all of the steps of the Box Method to complete the card. The cards could be sorted in a way that a specific group or individual students only solve one type of problem consistently until confidence and understanding is achieved before implementing the other card types.

Sample Scoot Cards

Math Stories in a Box

In this activity the students will fold a blank sheet of paper into four equal boxes just as if they were drawing the Box Method for binomials in their interactive notebooks. In each box, the student will illustrate an aspect of a self-created multiplicative comparison word problem. The students will then swap story boxes within their small group and repeat the activity until each student has had an opportunity to share their story. To ensure accuracy and further make the connection that the Box Method and the standard algorithm are related, the students will use the Box Method to solve the word problem and the standard algorithm to check their work.  The students will need to understand the row sum to partial product connection as illustrated in the example below. Upon completion, each group will choose one story to share with the whole class. The group must collectively teach the class (Students as the Teacher Strategy) how to solve the word problem using either the Box Method or standard algorithm.

9  × 4, 353 = 9  × 4,000  +  9  × 300  +  9  × 50  +  9  × 3 =

Box Method Example:

36,000 + 2,700 + 450 + 27 =

30,000 + 2,000 + 400 + 20

+ 6,000  + 700   +50  + 7 =

30,000 + 8,000 + 1100 + 70 + 7 =

30,000 + 9,000 + 100 + 70 + 7 = 39,177

U.S. Standard Algorithm Example:

3 4 2

4353

× 9

---------

39,177

The key observation here is that the product of a digit and a place value piece consists of at most two place value pieces, one of the same magnitude as the original piece, and one of one magnitude larger. The numbers in the first row are the partial products from the grids of the Box Method. In the second row, each number has been decomposed into a place value piece of the same magnitude as the part of the second factor it comes from and a place value piece of the next higher magnitude. The larger magnitude piece is above and the smaller one is below. It is as if the boxes have been partitioned in two sub-boxes, and the larger magnitude piece put on top, and the smaller one on the bottom. Next, to get the 3^rd row, the place value pieces of the same order of magnitude are added. This is like adding the contents of the boxes along diagonals in the more finely partitioned box. As indicated in the 4^th row, more regrouping took place before writing the final answer (on the right in the 4^th row).

If you compare this with the standard method, you will notice that the amounts in the top boxes are the “carries”, the numbers that get written as superscripts in the standard method, to be added to the product at the next place. Doing things like this and comparing might help students realize why, at each place, they should multiply first, and then add the carry to the product, rather than the other way around.

Since I will be sharing place value and multiplication picture books (tiered list of books provided in the resources section) with the students throughout this unit, having them create these mini stories will add to their ability to apply mathematics to connect both reading and writing. It also allows the students an opportunity to be creative with their illustrations, which at times can be a rarity for this grade level, especially in mathematics.

All of the activities above correspond with 2 digit by 2 digit multiplication as that is what the standards require for my students. However, each example can also be expanded on a larger scale with more digits later in the year for enrichment purposes.