Big Numbers, Small Numbers

Multiplication Basics

“When students are learning base-ten concepts, they are combining multiplicative understanding (each place is ten times the value of the place to the right) with a positional system (each place has a value) - something hard to do prior to learning about multiplication.”¹³

It is equally challenging for students to jump directly into solving multi-digit multiplication problems as required by the fourth grade standards in Virginia. So, before delving into multi-digit multiplication, let’s take a moment to review multiplying single place numbers. When thinking of a one digit number and any place value piece we can easily write: 3, 30, 300, 3,000, and 30,000 etc. which is equivalent to:

3 × 1 = 3

3 × 10 = 30

3 × 100 = 300

3 × 1,000 = 3,000

3 × 10,000 = 30,000

These same principles can be used to multiply one digit numbers and multiples of ten. For example:

180 + 24 = 204

6 ×34 = 204

In the example above we can see how the distributive property is used to multiply the 6 with each of the place value pieces of the 34 which was written in expanded form.

As the students move from single digits to two digit multiplication it is good practice to expose them to multiples of 10 and 100 beforehand. In Virginia this is generally introduced in third grade. Van de Walle¹⁴ articulates that, this focus supports the importance of place value and an emphasis on the number rather than the separate digits. By looking at the number, the student will be able to see the individual place pieces more clearly and thus decompose the number accordingly when working with larger numbers provided the student is able to keep track of place value.

For example:

19 × 80 = 19 × (8 × 10) = (19 × 8) × 10 = 152 × 10 = 1,520

Similarly, we can use place value to guide the computation of multiplication involving higher powers of ten as well:

19 × 800 = 19 × (8 ×100) = (19 × 8) ×100  = 152 × 100 = 15,200

Again, the distributive rule comes into play as the 19 is multiplied with each place value piece to arrive at the product for the given equation. When the student is able to visualize the place value pieces of powers of ten numbers the computation tends to be easier for the student to grasp and apply the concept to more real-life situations.

When looking at two digit by two digit multiplication and the role of zero as in the example below, the importance of understanding each place value piece increases in computing a product. This example models a frequent misconception amongst students who do not understand the role of the zero for the second row of partial products as well as the value of the “1” in the “13.”

Figure (c)

Compared to the correct algorithm:

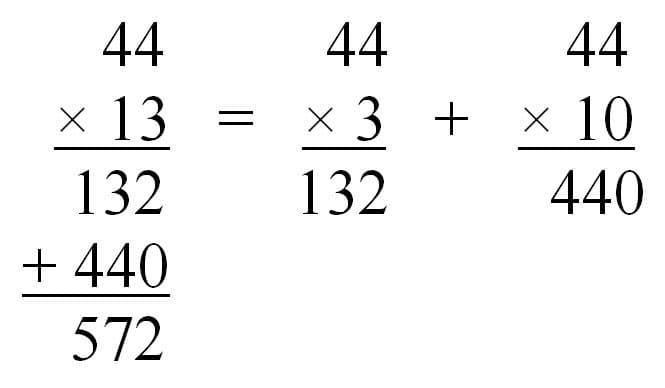
Figure (d)

In figure (c), one can clearly see that understanding that the “1” in the multiplier represents one ten which produces an increased value of the total product of the algorithm as evidenced in figure (d). Choosing not to identify the “1” as one tens caused the student to multiply it as another ones digit instead. Ignoring place value completely in this example is a common misconception amongst students in this age group. Figure (d) shows how the student was able to insert a “0” in the second partial product to indicate that the ones digit of the multiplier had already been multiplied with each number of the multiplicand.