Properties of Operations
Addition
In elementary schools across the United States teachers are constantly telling the students that we must line up our digits to add correctly. Why is it important to do this? Simply put, we must add like units. The ones should be added with the ones, tens with tens, hundreds with the hundreds etc. until all digit units have been summed together. On the lower elementary level and for visual learners it is best to use concrete models (Base-10 blocks etc.) to demonstrate this before moving the students to conceptual understanding. Lining up the digits ensures that we do add like units.
Prior to moving into multiplication, I plan to briefly review the properties of addition as they connect rather well with the properties of multiplication.
The Commutative Property of Addition says that changing the order of the addends does not change the sum.
33 + 66 = 66 + 33
The Associative Property of Addition states that the way in which addends are grouped does not change the sum.
33 + (66 + 99) = (33 + 66) + 99
The Identity Property of Addition states that the sum of any given number and zero is equivalent to that number.
99 + 0 = 99
Keeping these basic properties in mind, let’s shift our focus to the star of the unit.
Multiplication
Multiplication has properties parallel to the properties for addition.
The Commutative Property of Multiplication says that one can multiply the factors in any order and the product will not be affected.
369 × 33 = 33 × 369
The commutative property can be illustrated using a rectangular array. Using a rectangular array allows the students to see how each grid space represents one digit and is the product of multiplying the rows by the columns. Meaning 6 rows times 7 columns is equivalent to 42 grid spaces. In the figures below (a) represents 7 × 6 and (b) represents 6 × 7. Figure (b) is the result of rotating (a) 90 degrees, and yet both illustrations have the same number of grid spaces, therefore 6 × 7 is equivalent to 7 × 6.
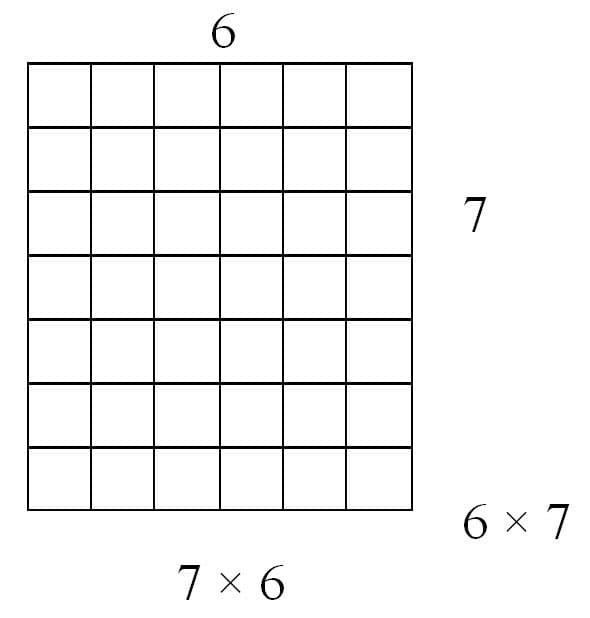
Figure (a)
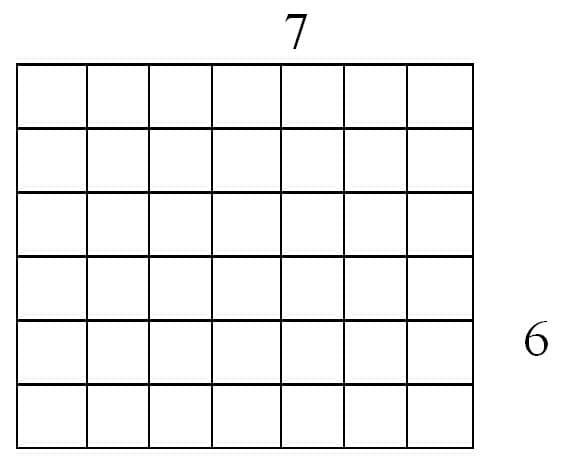
Figure (b)
Bennett et al10 emphasizes that, it is equally important to note that understanding the commutative property practically cuts the number of basic multiplication facts that students must learn in half. Giving the students, this foundational information will indeed assist them in solving more complex multiplication problems. Knowing the basic multiplication facts makes it easier for the student to multiply by the powers of ten.
More Multiplication Properties of Importance
The Associative Property of Multiplication says that, when three or more numbers are multiplied, the product is always the same regardless of their grouping. Thus, for example
(5 × 14) × 19 = 70 × 19 = 1330, and 5 × (14 × 19) = 5 × (266) = 1,330.
The Identity Property of Multiplication states that any number multiplied by one is that number.
369 × 1 = 369
The Distributive Property is the crucial property of arithmetic that connects multiplication and addition. It states that a multiplication fact can be broken up into the sum of two multiplication facts. We can decompose or “break one of them into parts, multiply each of the parts by the other factor and add the results.11” Let’s model the distributive property using the basic multiplication problem we used above in figures (a) and (b).
7 × 6 can also be calculated as 7 × 3 + 7 × 3 since 3 + 3 = 6.
The end result supports 7 groups of 6 which equates to 42. The 6 can be broken up in other ways as well such as (5 and 1) or (4 and 2). Due to the distributive property the product will continue to be equivalent no matter how the factors are broken up.
The distributive property can be modeled using an array. I will use 7 × 6 again for demonstration purposes.
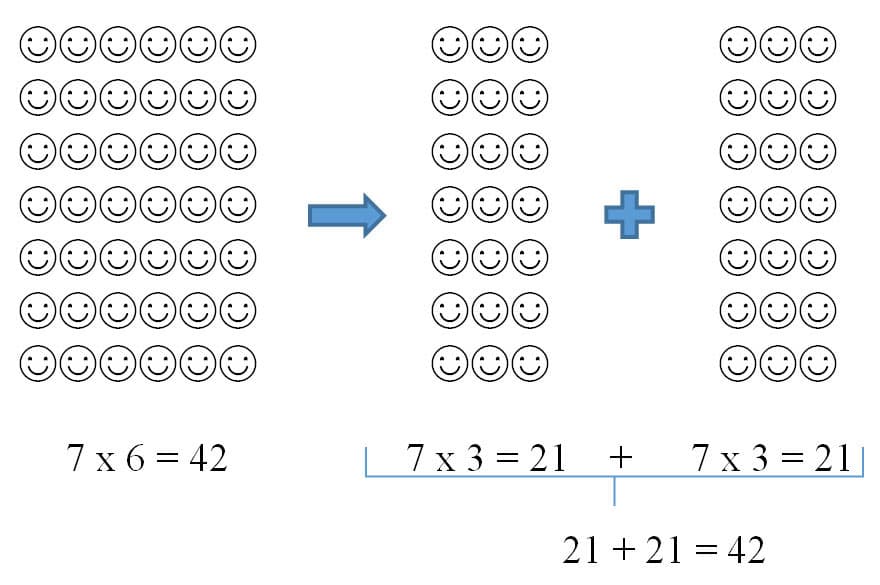
The Extended Distributive Rule per Howe and Epp 12 states, “If A and B are sums of several numbers, then the product AB may be combined by multiplying each addend of B by each addend of A, and adding all the resulting products.”
For example, if A = a + b and B = c+ d + e, then
AB = (a + b) (c + d + e) =
ac + ad + ae + bc + bd +be
Let’s look at this rule using the example: 45 × 239
(40 + 5)(200 + 30 +9) =
(40 × 200) + (40 × 30) + (40 × 9) +
(5 × 200) + (5 × 30) + (5 × 9) =
8,000 + 1,200 + 360 +
1,000 + 150 + 45 =
9,560 + 1,195
= 10,755
The example above allows us to link multiplication and addition through the Extended Distributive Rule while multiplying in base 10 form. Each row of the grid is the result of multiplying each single place piece of one factor by each place value piece of the other factor, and then adding all the results.
The Distributive Property, and more general versions of it, as in the example above, is the key to performing multi-digit multiplication.
The Zero Property of Multiplication states that any number multiplied by zero is zero. This rule is a consequence of the Identity Rule for addition and the Distributive Rule.
369 x 0 = 0
Zero is a digit that is often presented to students as having no value but instead occupies the role of a place holder. This can cause confusion for students when completing more complex multiplication computation such as multiplying 2 digit by 2 digit numbers. Zero in this context simply means that there is nothing in that place however; we will take in consideration how easily this misconception can alter the product in a later example.
Each of the properties above provides rules to help solve multiplication problems that will always apply to those specific equation types. Being able to identify the situations in which a property applies would be beneficial for a student who is just learning the basics of multiplication.

Comments: