Content Objectives
My student’s lessons will be based on the objectives listed below:
VA. SOL 3.8
The student will estimate and a) measure the distance around a polygon in order to determine its perimeter using U.S. Customary and metric units; and b) count the number of square units needed to cover a given surface in order to determine its area.
VA. SOL 5.8
The student will a) solve practical problems that involve perimeter, area, and volume in standard units of measure; and b) differentiate among perimeter, area, and volume and identify whether the application of the concept of perimeter, area, or volume is appropriate for a given situation.
Modelled Sample Geometric Methods
Initially, students will receive extensive, direct instruction on all three concepts (perimeter, area , and volume, beginning with the formula for one dimensional figures for a day or two and progressing to the other concepts in the same manner) to include mini lessons, teacher modelling, related story books and or song/video use that also exemplify methods of using the concept, hands on exploration with the use of manipulatives, exploration of digital game play, and old fashioned board game play, as well as geo-talks between classmates, as well as worksheets as practice assessments. Students will be given numerous figures of varying sizes in order to carry over all concepts and procedures learned. The tasks indicated here will be mentioned in detail later in this unit.
The following is a sample lead in (mini lesson) and exercises (see figures A-C) for day five of the unit. The lesson will be implemented in order to activate prior knowledge of the geometric concepts of perimeter and area that were taught earlier in the week. The activity will begin with perimeter and I will instruct my students as follows:
“When thinking about perimeter, think about the following: perimeter is a, ‘linear’ measurement. The perimeter is the total of the lengths of the sides of a figure. Think of starting at one corner of the figure and walking all the way around it until you get back to your starting point. The distance walked is the perimeter of the figure”.3
An anchor chart that I will create in the classroom with the students will feature a man or woman walking around the outside of a figure with the word perimeter in bold print.
“The students will have a permanent picture in their minds and will remember to focus on the outer boundary of the figure when performing calculations pertaining to perimeter”.4
The students will be presented with the following mini exercises:
I will initially review the vocabulary to re-familiarize the students with the terms and meanings, as something similar to the exercises below will be provided to the students on or around day
five.
Vocabulary: perimeter, area, volume, array, dimensions

Figure A. ( Use the box to find the perimeter ) box constructed from word
a) What is the perimeter of the box (figure A)? The students should be able to determine fairly quickly that the perimeter is 12 units. Discussions would require the students to reiterate why they know that 12 units is the correct answer, which will include thoughts about the formula for perimeter and how to apply those concepts to finding the perimeter of the above box. I would include an additional exercise that changes the dimensions of the box and direct the students to solve for perimeter.
Upon my satisfaction (as there are numerous perimeter exercises to choose from, for example, geo talks, journal entries, online digital game play) with the oral responses and written evidence that my students provide with perimeter, I will move on to the next part of the activity. It will focus on area and I will instruct my students as follows:
“When thinking about area, think about the following: area is a ‘square’ measurement. The area is the surface of the object. Area answers questions such as, how much paint do you need to cover a surface, or how much grass seed do you need to seed a lawn?”.5
An anchor chart will be created with the students in the classroom that features a fenced- in section with the words, area, appearing in big, bold letters, inside or on top of the fenced- in section. I will ensure that the students understand that they are to count the units inside of the figure when solving for area.
b) How many boxes are within the larger rectangle (figure A) or what is the area? The students should determine that based on the interior of the box, there are four rows of two boxes for an area of 8 units.2 Students will most likely count one by one, however, with more practice they will soon become more familiar with multiplying, although most area exercises will be scaled back to smaller dimensions due to their skill levels. Students will be asked to identify what formula they solved for. The students should respond by saying ‘area’.
Next, within a few days of implementing the above exercises and additional exploration, the students will be presented with polyominoes. There are twelve groups of polyominoes, however, specifically for this unit study, we will use pentominoes. Students will be asked to identify the perimeter as well as the area of each figure of each pentomino (see figure B). A detailed discussion covering pentominoes will be addressed later in this unit study, however, the exercises below will follow a detailed presentation of pentominoes within the classroom.
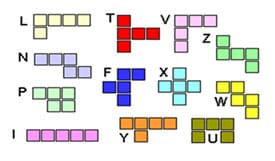
Figure B. (Use the above figure to find the perimeter and area of each pentomino)
The students should walk away from this exercise with the understanding that despite the fact that each group contains five, hence the name- pentomino, the rearrangement will cause the area to hold constant to five units2, however, the perimeter will not remain constant and the students can determine which pentomino arrangement will yield a different perimeter from the others.
After viewing the various pentominoes during whole group, the students will work with a partner to explore the various transformations (rotations, reflections and translations) of the pentominoes as well as the area and the perimeter. They will be directed to journal in their notebooks about the exercise concerning what they learned and provide information about pentominoes and the various transformations as indicated above in order to detail all that they have learned about pentominoes.
Upon my satisfaction with the oral responses and written evidence that my students provide with area, I will move on to the next part of the activity. It will focus on volume. I will instruct my students as follows:
“When thinking about volume, think about the following: Volume is a ‘cubic’ measurement. Volume is the number of cubic units needed to fill a given solid”.6 Volume answers a question like, how much space is occupied inside of a solid, 3 dimensional object. An anchor chart will be created in the classroom with the students that features cubes of varying sizes. The cubes will be broken up into three rows, highlighting the columns as well. The cubes will display the dimensions of length, width, and height. The chart will remind the students to count the amount of cubes in each of the rows which will also account for the columns. The chart will indicate that students should perform repeated addition in order to obtain the volume. Emphasis will be placed on the idea that the total number of cubes that are accounted for match up with the total number acquired after counting the amount per row. This is demonstrating how to identify the amounts for length, width, and height. Although my students will view a pictorial version of a three dimensional object, they will also be presented with a hands- on three dimensional object.
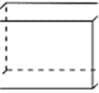
Figure C. (3 dimensional cube)
Students will use cubic square blocks. The blocks will be used to derive the volume of the 3-D object in figure C., with similarities to the one above. Students may also encounter an exercise such as, the one below. When completing a technology assignment (Figure D), such as the exercise below, it will follow the same procedure in determining the volume that my students will us to find the volume for figure C.

Figure D. (A technology exercise)
My students will be expected to recall that they are to use repeated addition and add the amounts of the rows and columns which will be: 6+6+6+6+6 and yields a volume of 30 units.3
e)Describe how to find the volume of the cube.
By the time that students are asked to complete this task, they would have had 1-1 ½ weeks to become familiar with volume. The students would be expected to provide me with as much information as they can recall concerning volume, such as identifying that using cubed blocks to identify the length, width, and height is the way to proceed since volume is three dimensional. Students should be able to recall that they will count the amount of blocks that are in each row, and perform repeated addition to identify the volume in cubic units.

Comments: