Perimeter, Area, Volume, and All That: A Study of Measurement

Curtailing Misconceptions

Similar to the need for preliminary skills that students must have to perform grade level tasks, I will be on the lookout to help them to avoid pitfalls commonly called misconceptions.

“Consider the following situations involving perimeter, area, volume and children’s misconceptions. What can teachers do to help them to understand correctly? Let’s explore a few common misconceptions.  Misconception: Andi says that the area you can make with sixteen tiles (figure F or some similar square) is always bigger than the corresponding perimeter, because working out area uses multiplying, but working out perimeter is just adding lengths”.¹¹

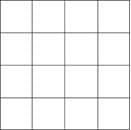
Figure F. 4 x 4 square

Perimeter- count to add sides, Area-count the inside boxes of the large box P=16 units, A= 16 square units 

Figure G. 2 x 2 Rectangle

Perimeter= Count to add all sides

Area-count the inside boxes of the rectangle

P= 8 units, A=4 square units 

“Intervention: The teacher must provide the intervention, by trying different rectangles to find some suitable counter-examples”.¹² The units of area and perimeter are different and therefore they should not be compared and to do so is a mistake. The above, square A is 4x4 square units. It shows that while the area is equal to sixteen square units, the perimeter is also sixteen units. Andi would be encouraged to work through finding the perimeter and the area in order to make sense of his error, as he stated that the area would always be greater than the perimeter because of the multiplication involved with area. Additionally, the students will be asked to construct the following rectangles: 1x16 of which the perimeter of 34 units is larger than the area of 16 units² and 2x8 of which the perimeter of 20 units is larger than the area of 16 units.² Rectangle G is 2x2. It shows that while the area is four square units, the perimeter is actually greater than the area which is once again contradictory to Andi’s assumption.

“Another method for this issue is to point out that the standard formula for the perimeter of rectangles includes multiplication. Andi may not understand the algebraic formula P = 2 × (L + W), but may be helped to see that there is a doubling of the sum of length and width; obviously doubling is like multiplication — in fact, it is multiplying by two. Since this shows that both perimeter and area involve multiplying, maybe the initial argument is not as solid as Andi thinks”.¹³

Andi should be led to conclude that it doesn’t make sense to compare length and area. There is also substantial reasoning behind ensuring that Andi is aware of the fact that length and width must be multiplied twice or at least counted twice and has to do with the fact that one should be aware that the opposite sides of the figure are alike. This lessens the frequency of errors, as I have observed students miscalculate when they aren’t focused, for example, P=4+5+7+8, as opposed to the actual dimensions P=2(4+4) + (7+7). The former calculation is impossible since opposite sides of the figure will always be the same. Students also think in the following ways:

H. (lopped rectangle)

“Misconception: Collen says that the area in this “lopped” rectangle is eighteen square cm, (see figure H). Intervention:  Draw a sketch plan, or even a precise centimeter-square grid; or use a geoboard (a rectangular array of nails, using rubber bands to loop around corners of figures). A geoboard is an invaluable aid for teaching area and perimeter, because it allows easy construction of geometric figures, and easy counting of units of length and units of area.  Mark the centimeter scale along the top portion of the lopped rectangle (figure H), as well as the bottom portion of the lopped rectangle, and draw the square grid pattern over the figure. Count the number of unit squares of area”.¹⁴

I will be sure to always reiterate to my students that when we find the area of a figure, we are focusing on the inside portion of the enclosed area of the figure.

With the routine review and practice of various geometric exercises, the misconceptions will most likely occur less frequently.  I am aware that practice makes perfect therefore continuity of these skills is essential.  Students will be able to reason and problem solve without getting stuck as routinely as they once did.

As a result of my research, I found much of what I learned to be very helpful in preparing lessons for my students. I plan to help my students begin to think about transferring the skills of the measurement of perimeter, area, and volume acquired within the lessons that I implement to higher level thinking tasks. By transferring those skills, the students will be able to perform the calculations within the upcoming assigned project. My intentions are for the students to not only be able to transfer the skill of calculating perimeter, area, and volume of a   given object, but they should also be able to generalize and make application of those same skills to perform other higher level thinking exercises, (i.e. geometric formula measurement of triangles, trapezoids, and even cylinders, etc.) as they move on to higher grade levels. 

Students will eventually (at this time, the students are not ready to perform calculations as they are too complex) come to the realization that perimeter, area, and even volume concepts are experienced during real life situations, as students will eventually be faced with situations where they will have to help their parents/relatives/friends identify the measurements of: walls that require painting (area), or floors that will undergo the installation of carpeting (area), or shingles that are to be replaced on the roof (area), or being faced with identifying which belongings that they own will fit into a moving truck when relocation is a reality (volume), and upon arriving to their new residence there may be an interest in purchasing a fence for the yard (perimeter). The above mentioned concepts are tasks geared toward older children and the idea is for the exercises and activities within this unit to be used to prepare the student to eventually be able to complete those higher level, more complex tasks. The more students are provided with practice that entails geometry (much like the other academic topics that are addressed in school which act to prepare the student for real life), the more comfortable they will be at handling various tasks in their life of which natural math will play a part.