The Extended Distributive Rule
The extended distributive rule is derived from the basic distributive rule (for either factor), plus multiple uses of the commutative and associative rules for addition. In discussing the extended distributive rule, the symbols for multiplication (× and •) will be removed; the numbers/quantities that are to be multiplied are placed side-by-side.
The Extended Distributive Rule
A and B = sums of some numbers
AB = sum of (any addend of A) ×(any addend of B)
The final product will be determined by adding all the resulting products of AB
We can call this rule Each with Each (EwE): you multiply each addend of A with each addend of B, and sum of all products.
Let A and B be defined as,
A = (a + b) and B = (c + d)
|
AB |
= |
(a + b) (c + d), |
substitution |
|
= |
(ac) + (ad) |
first a is multiplied by c and d |
|
|
+ (bc) + (bd) |
then b is multiplied by c and d |
||
|
= |
ac + ad + bc + bd |
the sums of all products are added together |
Note that this gives exactly the same sum as FOIL. However, it is valid for sums with any number of addends, while FOIL applies only to products of binomials.
Example #11:
As an Area Model: Multiplying a sum of 2 variables by a sum of 2 variables
A = (a + b) and B = (c + d)
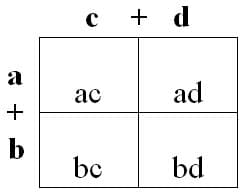 = (ac) + (ad) + (bc) + (bd) = ac + ad + bc +
b
= (ac) + (ad) + (bc) + (bd) = ac + ad + bc +
b
Example #12:
Area Model with Numerical Values: Multiplying a sum of 2 numbers by of 2 numbers
(12)(25)
12 = (10 + 2) and 25 = (20 + 5)
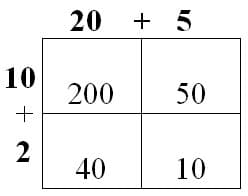 = 200 +
(50 + 40) + 10 = 200 + 90 + 10 = 200 + 100 = 300
= 200 +
(50 + 40) + 10 = 200 + 90 + 10 = 200 + 100 = 300
Due to the basic arithmetic ideas of the distributive, commutative, and associative rules, numbers are able to be written in any way (as long as the place value is maintained), while arriving at the same product. In the numerical example above, you can see that the products of the various place value parts are just the products of the powers of ten times the products of the digits. To better illustrate that statement, here is a visual representation below:
Example #13:
(25)(12)
(2.5 ×101) (1.2 × 101) = (2.5 × 1.2) (101 × 101) = (3) × (102) = 300
This can be justified because of the Product Rule of Exponents as defined as: “The powers of 10 stand in a multiplicative relationship to each other. If we multiply one of them by 10, we get the next one. Product rule for exponents: 10m × 10n = 10m+n, for any whole numbers m and n.” 4 The Law of Exponents is not required to be explored in depth in this unit as it will be previously explored and taught prior to the start of this unit, as it governs how powers of the variable are multiplied together. However, there are vital ideas as it relates to the quantities of exponents. These ideas will be investigated prior to this unit to ensure the background knowledge is acquired that will allow students to accurately apply the operations of polynomials.

Comments: