The Commutative Rule of Multiplication
The commutative rule is a rule of addition, and also of multiplication. For multiplication, it states that you can multiply 2 factors in either order without affecting the product.
Probably the best way to develop an intuitive sense for the rule is through the Array Model. This model is also important because it helps prepare students develop intuition of the concept of area.5
The best way to visualize the commutative rule is thinking of taking an array model where two factors are being multiplied, and reflecting the array over its diagonal (or rotating it by 90o). Then the size of the array, which equals the product of both factors, remains the same. The same can be done when representing multiplication by the area of a rectangle.
The Commutative Rule of Multiplication: For non-negative integers, a and b
a × b = b × a
Example #10:
The Commutative Rule of Multiplication: For non-negative integers, a and b
14 × 113
let a, and b be defined as a = 14, b = 113
|
14 × 113 = 1582 |
113× 14 = 1582 |
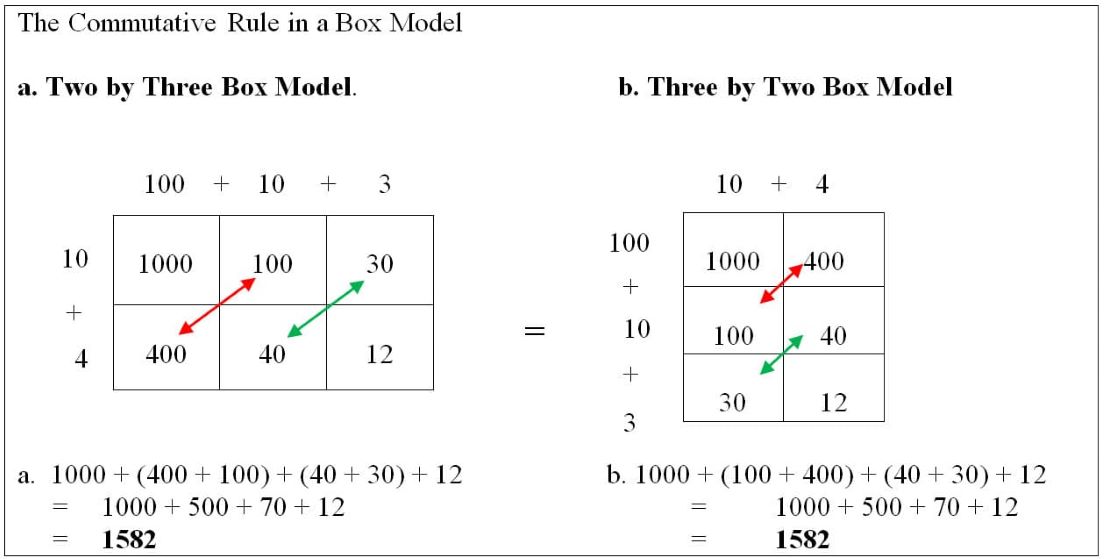
Above, observe that I am using the extended distributive rule to evaluate each product. It should be emphasized that the extended distributive rule is consistent with the commutative rules of multiplication and addition. It illustrates that by applying the arithmetic rules of multiplying using the commutative rule, you will obtain the same product regardless of the order of the numbers being multiplied. The same sums of products can be seen in both calculations a and b above.

Comments: