Perimeter, Area, Volume, and All That: A Study of Measurement

Activities

Side – By – Side Analysis/ “And then what”

Objective: Justify how the associative and commutative rules prove their calculations of products of polynomials to be correct. Demonstrate multiplying polynomials using area models and the box method.

Days Covered:  3–4 Days / 6-8 Rotation Schedule

Using this activity will provide parallel learning and exploration for students. This strategy is intended to be used in the beginning of the unit. Before formally introducing the idea of multiplying polynomials but after reviewing area models with numerical values.

Figure 5: Side by Side Anchor Chart for Student Reference

These activities will allow scholars to see the relationship with the place value/base ten parts and the x or other variables used to represent each polynomial. There will also require some time for structure math talk/discourse however, conversation will be concentrated on solidifying the general principles of arithmetic: associative, commutative and Any Which Way rules of multiplication, the Law of Exponents, and the distributive and extended distributive rules. The side by side examples should be scaffolded in a number of ways that allow students to make comparisons and begin justifications. These examples should be organized in a way that explicitly demonstrates that the same multiplicative rules apply for polynomials. Each rule is valid for all numbers and therefore for variables, since variables simply represent numbers. It is imperative that students are familiar with the Law of Exponents, particularly the Product Rule, to guarantee student understanding and accuracy with each task.

Multiplicative Rules with Polynomials

The Distributive Rule of Multiplication: For non-negative integers, a, b, and c

a × (b + c) = (a × b) + (a × c) 

let a, b, c be defined as a = 2, b = x, c = 2

2 (x + 2)

(2 • x) + (2 • 2) = (2x) + (2 • 2) = 2x + 4

The Associative Rule of Multiplication:  real numbers, a, b, and c

a × (b × c) = (a × b) × c

let a, b, c be defined as a = 2, b = 3, c = x

2 • (3• x)  =  (2 • 3) • x = 6x

It should be noted that when thinking of the associative rule of multiplication, we could look at the rule as a symbolic way of saying that we can compute the volume of a cube as base times height, or as length times area of side. The associative and commutative rules often get used together to justify the any which way rule.

The Commutative Rule of Multiplication: For non-negative integers, a and b

a × b = b × a

let a, b be defined as a = x, b = 3

x • 3 = 3 • x = 3x

let a, b be defined as a = (x + 2), b = (x + 4)

(x + 2) (x + 4)

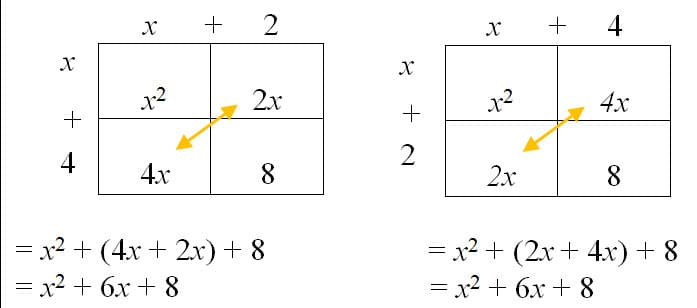
Example #13:

If… 2 (3+7) = (2)(3) + (2)(7)

= 6 + 14

= 20

Then… x (x + 2)

Example #14:

If… 4 • 3 • 8  =  (4 • 3) • 8  =  4 • (3 • 8 ) 

96  = 12 • 8  = 4 • 24

= 96  = 96 

Then… x • x² • 2x

1. After completing the above examples, what did you notice was similar? What about the process/equation was different? What evidence can you provide/offer to clarify your statement?
2. Can you and/or your partner find an alternative way to arrive to the same product? Draw/create your new model in the space provided.

Example #15: 

(x⁵)

define x⁵ = x · ((x · x) · (x · x))

1) Show that x² • x³ = x⁵, using the associative rule.

Example #16:

(x + 4) (x + 2)

A teacher asked 2 students to find the product of the above polynomials. Raven and Lillie demonstrated their work and responses below. Note your observations about their work, be prepared to discuss.

Raven:

= x² + 2x + 4x + 4 = x² + 6x + 4

Lillie:

(x + 4) (x + 2)

(x · x) + (x · 2) + (4 · x) + (4 · 2)

x² + (2x + 4x) + 4

x² + 6x + 4

With your partner please use the guided questions to make conjectures about the above examples.

1. What similarities do you notice in their work? What differences do you notice?

2. How were both students able to arrive at the same product if they multiplied the factors differently? How can your explanation be justified?

3. Are there other ways to multiply these factors and prove the product to be accurate?

4. Come up with at least one other way to demonstrate this process.

It should be noted that these types of problems will increase in difficulty, allowing my students the same experience with examples where the coefficients are greater than 1. An extension idea for students who grasp this concept quickly would follow:

5. Suppose the students were asked to multiply: (2x + 2) (2x+4); recreate the methods used by both students to find the product.

6. Aries noticed that 2x+2 = 2(x+1) and 2x+4 = 2(x+2). She said: I can get the same answer by multiplying (x+1)(x+2), and then multiplying all the terms by 4. Do you agree with Aries? Carry out her procedure.

There will also be a number of opportunities for students to solve problems and make connections with the parallels of multi-digit and polynomial multiplication. Below are a few examples that I will use to demonstrate multi-digit multiplication in parallel with polynomial multiplication. Examples like these will be used to make a point to ensure students agree when x = 10. Using examples that we’ve previously used will assist in making this point, as shown below.

Example #17:

If…

(x + 4) (x + 2) =  x² + 6x + 4

Then… when x = 10

(x + 4) (x + 2) = 14 × 12

= (10 + 4) (10 + 2)

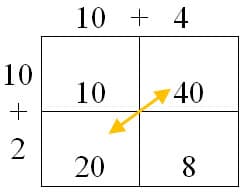
10² + 6(10) + 8 = 100 + 60 + 8 = 168

Example #18:

If…

x (x + 2) = (x )( x ) + (x )(2) =  x² + 2x

Then… when x = 10

x (x + 2) = 10 (10 + 2)

= 10² + 2(10) = 100 +20 = 120

Example #19:

If…

(x + 3) (x² + x + 2)

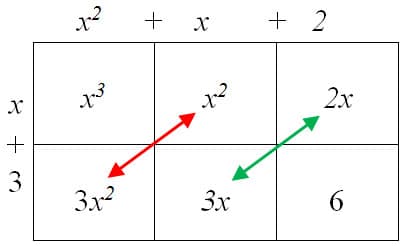
x³ + 4x² + 5x + 6

Then… when x = 10

(x + 3) (x² + x + 2) = 13 × 112

= 10³ + 4(10²) + 5(10) + 6

= 1000 + 4(100) + 50 + 6

= 1000 + 400 + 50 + 6

= 1456

Example #20:

If…

(x^-3) (x + 4)

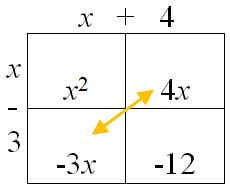 =  x^{2 +}x ^-12

Then…  when x = 10

(x^-3) (x + 4) = (10^-3)(10 + 4)

= 10²  + 10  ^-12

= 100 + 10  ^-12

= 98

Flip-Side

Objective: Find the area and perimeter of a rectangle with polynomial side lengths

Days Covered: 1-2 Days / 2-4 Rotation Schedule

During this activity students will be given the opportunity to use their knowledge of finding the area and perimeter of rectangles and irregular shapes with both numerical and variable side lengths. Students will be either paired up or in small collaborative groups to allow discourse and accountable math talks to happen. Each pair/group will be given approximately 5-10 sheets of paper that have the same rectangle or irregular polygon on it. Side A will represent numerical side lengths while on the flip-side, Side B will display the same shape only this time using variable side lengths. This activity is meant to allow my students to realize that the process in determining the area and perimeter is the same no matter the value of each side length. In the example below, you can see the contrast between both sides.

Example #1

1. Find the area of Shape A & Shape B.
2. Describe how Shape A aided in finding both measurements on Shape B.
3. Compare your work with another student; did you use the same process to solve? Arrive at the same answer? Justify how you both got the same answer by defining one of the arithmetic rules for multiplication.

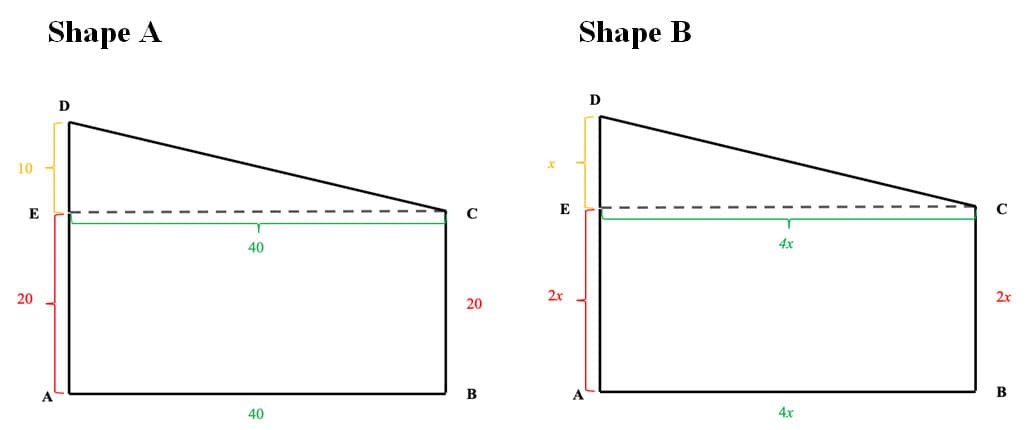
These examples can be customized for any student on any cognitive level. I will use colored paper and letters to label groups of problems based on the needs and academic reach of each of my students. Once identified students will be grouped homogeneously to ensure accessibility and engagement. Through proper facilitation the determination to move into heterogenous groups will be made.