The Unit Circle, the Symmetries of a Square and Dancing
It is necessary for the understanding of this unit to provide the ideas of what a unit circle is and what the Symmetries of a square are.
The unit circle is the name given to a circle with radius equal to 1. The unit circle is usually placed with its center at the origin of the coordinate system. In other words, analytically its center is O(0, 0). The unit circle is used in trigonometry to easily graph all the trigonometric functions, but in this unit we will refer only to sine and cosine.
We will also think of the square as sitting in the coordinate plane, centered at the origin and with sides parallel to the coordinate axes. We take the side lengths of the square to be 2, equal to the diameter of the unit circle, so that the unit circle just fits inside the square, and is tangent to it where both intersect the coordinate axes. See the figure below.
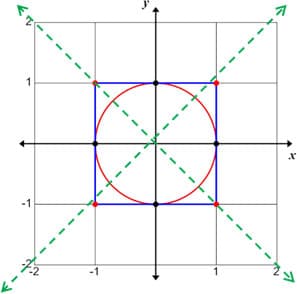
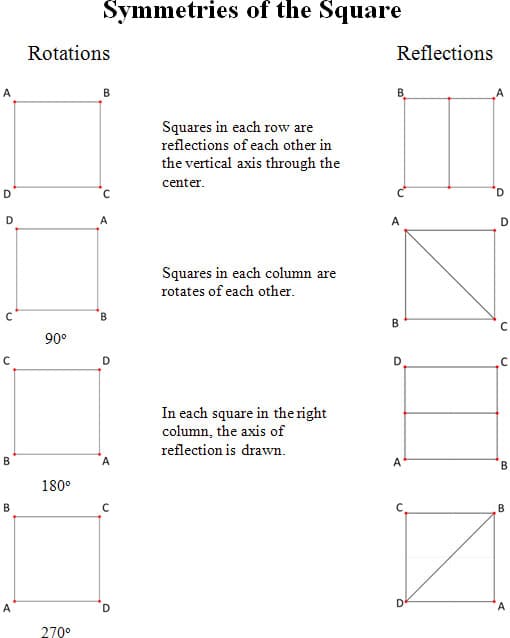
The square has reflection symmetries and rotational symmetries. To see if a square has symmetry with respect to a line, we apply a reflection over the given line. If the properties and characteristics of the square are preserved, then we say that the square has symmetry with respect to that line. With our standard square as described above, we can see that it has four lines of symmetry. It is symmetric across the coordinate axes, x = 0 and y = 0, and also across the diagonal lines y = x and y = x.
"In geometry and linear algebra, a rotation is a transformation in a plane or in space that describes the motion of a rigid body around a fixed point. A rotation is different from a translation, which has no fixed points, and from a reflection, which "flips" the bodies it is transforming. A rotation and the above–mentioned transformations are isometries; they leave the distance between any two points unchanged after the transformation."
From Wikipedia, the free encyclopedia
The square is also preserved by certain rotations around the origin. The angle of rotation can be 90 o, 180 o, 270 o or 360 o. This last value will place the square back to where it was at the beginning. It is the same as rotating by 0 o; that is, not moving it at all. We call this the identity transformation.
While researching how to implement the concepts of symmetries of the square that we learned in the seminar of "Math of Wall Paper," I came across applications in dancing. It is interesting to see that the re–positioning of the vertices of a square after each reflection produces similar movement as those done in a dance. If a dancer gets situated on each vertex of a square and then we apply all the reflections using the symmetries of a square, we will have the different positions that a group of dancers would have.
These ideas are most relevant to the type of dancing called square dancing. In square dancing, four couples start by standing at the corners of a square. As the music plays, they execute various movements, following the instructions of the person leading the dance, known as the caller. Each movement is a call. Many calls involve rather complicated motions, but some of the simpler ones are related to symmetries of the square, and could provide a way to connect dancing with learning about symmetries of the square.
Some of the simplest square dance calls involve each couple doing something in its own corner. Examples are dosado, with each couple walking around each other, facing the same way all the time, so that they are back–to–back when passing behind each other. There is also the swing, in which the couple holds each other as the pivot around the point halfway between them. Allemand is when they grasp hands or forearms while turning around each other.
In more complex calls, couple change places, or sometimes just the ladies or gentlemen change places. A call involving rotation is a Promenade, where each couple joins hands and walks side by side around the circle. In a Right and Left Grand, women face one way, and men the other and they walk forward clasping hands as they pass. In term of symmetries of the square, the men are rotating in one direction, and the women in the other. Usually, everyone walks all the way around the circle and returns to their original position, illustrating that rotation of 360 o gives the identity transformation. In a Ladies Chain, the women will all join hands with the ladies from the couple on either side, and walk sideways around the circle.
Right and Left Through is a call in which couples pass each other to assume the place of the other. If two pairs of couples on two opposite sides of the square do it, the square is reflected in the perpendicular bisector of the sides. If this is done with one pair of opposite sides, then another, the result would be rotation by 180 o. If a pair of couples on opposite corners of the square does it, the square is reflected in the diagonal. Doing this with one pair of opposite couples, and then the other will again produce a rotation by 180 o.
By doing these and other calls, students could produce any symmetry of the square. They could be challenged to predict what symmetry would be produced by a specific sequence of calls. If they got to be experts at this, they could be challenged with calls that produce more complicated permutations. This could be a great combination of dancing and math!
Being able to combine math, music and art in a lesson or a set of lessons that would start with patterns, sequences and series is keeping alive the dream that any teacher has, which is to be able to reach all students in a classroom, not only those who already like math, but those who struggle. I have always thought that a student does not need to be a genius to learn math. This is as well my personal dream, since I had the intention to become a musician since I was a child, but I was denied that opportunity. However, I have succeeded in keeping my dream alive and I want to be able to transmit that hope to my students combining my two passions, teaching math and music.
Now, if a student is able to understand the process involved in expressing steps of dancing, the next step would be to use that knowledge to understand the concept of motion using trigonometry, and therefore, expose students to the option to take more advanced math classes. In this case, the next level of math would be AP Calculus.

Comments: