The Mathematics of Wallpaper

Planning for Trigonometry

Lesson probably will be introduced in the second half of the second semester when the concept of the Unit Circle has been already taught. Combining a coordinate system and analytic geometry from Algebra–2, plus the new ideas from trigonometry such as sine and cosine functions in the unit circle, will help to have an anticipatory set.

To start de actual lesson, students will do the warm–up activity being reminded of the concepts already learned in previous math classes. At his point we have covered already concepts from the first semester. The warm–up will consist of exercises reviewing the positioning of sine and cosine of 45 ^o using the unit circle, reflection of functions over the lines y = x and y = x, equivalence between graphing a point in the unit circle and the corresponding coordinates from a coordinate system. Vocabulary will be introduced to remember lessons from Algebra–II and geometry as well from previous years. The activity should take approximately 20 minutes including teacher's explanation or students presenting their solutions on the board.

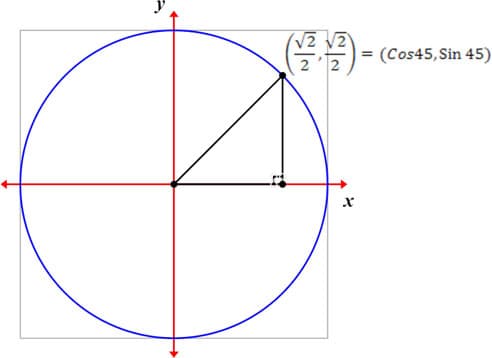
The next 15 minutes will be used to explain the relationship between trigonometric identities and the unit circle. Given and angle with initial side at the x axis and terminal side anywhere between 0 ^o and 90 ^o, we can represent sine of the given angle as the vertical segment from the circle towards the x axis; and cosine of the same angle as the horizontal segment from the circle towards the y axis.

On the next 15 minutes, the demonstration of the identity sin ²θ + cos ²θ = 1 will be done. The first part is to apply concepts from Geometry such as trigonometric ratios and algebraic expressions to be able to demonstrate the identity. The second part is to apply the unit circle and the graphic approach of sine and cosine to demonstrate the identity.

To prove the identity sin ²θ + cos ²θ = 1 using the unit circle, we can include the theorem of Pythagoras, and conclude that the addition of the squares of the two segments, vertical and horizontal described on the previous paragraph will be equal to the square of the hypotenuse, which in this case is exactly the radius of the unit circle. By default, because the radius of the unit circle is 1, the addition sin ²θ + cos ²θ will be l.

As well as the above identity, there are others that could be verified using the unit circle. One would just need to relate the identity with the Pythagorean Theorem.

The geometric representation of points in the unit circle using trigonometric terms is similar to the representation using analytic coordinates. For one side, in Algebra–II, I will be able to present the curriculum unit just using Algebra, for Trigonometry, I will be able to use sine and cosine. For example, for square dancing, the vertices of a square to represent the presence of 4 people, one on each vertex can be as well represented using sine and cosine. Using sine and cosine instead of algebraic analytic coordinates provides more flexibility for the "dancers" to move. If the position where the dancers are located varies on the circle, the angle will change. It is important to understand that there will be a fixed distance between partners while dancing.

On the following graph, the same representation is given using coordinate values and trigonometric expressions. This graph is just an example of what can be done. Although x could be any value, I have chosen the value of x = 45 ^o as an example.