The Mathematics of Wallpaper

Restricting the Domain to get Inverse Functions

As the second example above shows, the inverse relation of a function is not always a function. However, sometimes if we restrict the domain of a function to a smaller set, the inverse of the restricted function is again a function. For instance, in the second example above, if we restrict the function x → x ² + 3 to the domain x > 0, then the inverse relation will consist only of the top branch of the graph of the full inverse relation. This branch of the graph does satisfy the vertical line test, so it defines a function. This idea is used for defining important functions, including the inverse trigonometric functions.

In Algebra–II and in Trigonometry, we study the inverse of trigonometric functions. To be able to define them, the domain of the original trigonometric function has to be limited to a small part of the original domain. We can see on the attached graph that when the function y = sin x is "inverted," the new graph becomes the reflection of sin x over the line y = x. This reflection occurs because all the elements (a, b) of the function are being switched to (b, a). Therefore when graphing the inverse function, the x–axis becomes the y–axis and the y–axis becomes the x–axis. Therefore, to define the inverse function y = arc sin x, we limit the domain of sin to the interval from π/2 to π/2. The inverse of this restricted function is again a function. Similarly, to define arccosine, we limit the domain of cosine to the interval from 0 to π.

It is important to mention that students need to be taught the different ways that books, teachers and calculators use for symbols for the inverse of trigonometric functions.

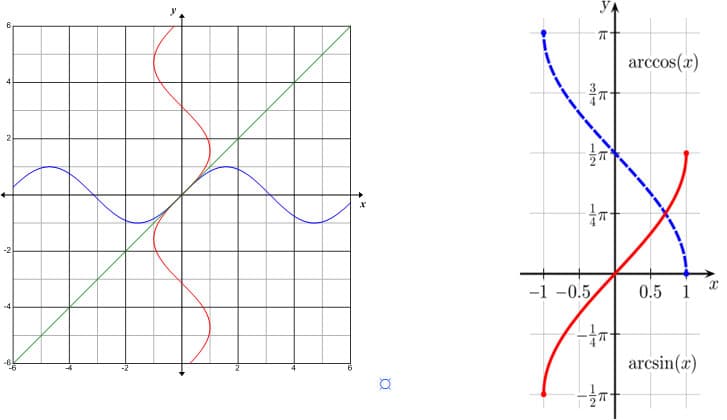
When the trigonometric function y = sin x is inverted, interchanging x for y; the result is not a function.

The first graph illustrates the reflection of the graph of the function y = sin x in blue color over the green line y = x. The red curve is the graph of the relation y = arc sin x; obviously, this red graph badly fails the vertical line test, so the result of this reflection does not produce a function. Therefore, to continue with the study of functions, the domain of sin x must be limited. We can see those limitations on the graph next to it.

The second graph illustrates the limitation of the domain of y = arc sin x in red color and y = arc cos x in blue color. One can see that for y = arc sin x, the domain has been restricted to [–π/2 , π/2 ]

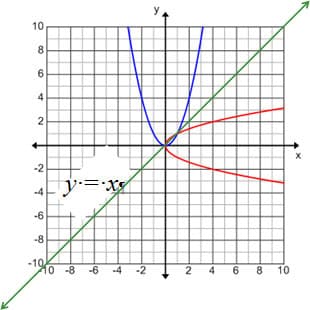
Similarly, when certain functions such as the ones who come from the parent function y = x ² are inverted; the result is not any longer a function. If one follows the algebraic instructions to inter–change "x" for "y" the new algebraic expression would be x = y ². Then, when solving for y, one would have y = ±√x. However, only the positive or the negative portion of the expression represents a function. In the figure below, the function in blue color is f(x) = x ² and the "inverted" function is shown in red color.

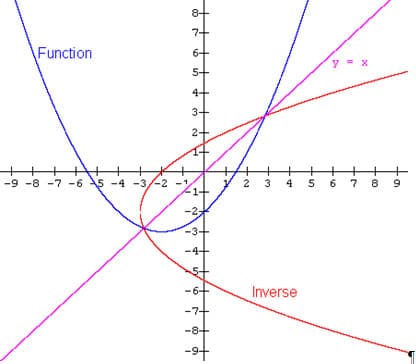
Another example is shown below. The function in blue color is f(x) = 1/4(x + 2) ² 3 and in red color, the result of inter–changing the x for y is shown as the inverse of f(x). However, in both examples the resultant is not a function; therefore, the graphs have to be limited to only the top or bottom portions exclusively.

In the first example, to preserve the concept of function the domain of y = x ² can be limited to x ≥ 0; therefore, the inverse y =√x would be a function with domain x ≥ 0 and range y≥ 0. In other words, it would be the upper side of the red curve. On the other hand, if the domain of y = x ² is x ≤ 0, the inverse would have the domain x≥ 0 and the range would be y ≤ 0.

The graph of an inverse function can help to create patterns obtained by reflecting a given graph over the line y = x and therefore, being able to use the new graph in an artistic design. Designs are usually used to create wallpaper, shirts and other patterns applied to fabrics. This idea can be developed as well with the lessons involving patterns and sequences.