What is a fraction?
Fractions can be a stumbling block for many students. There are two points that can be relevant to this:
i) Students need to revise their understanding of what a number is: from a counting or additive conception to a ratio or multiplicative conception. A number line is a description of the relative size of a given quantity, as measured by another quantity of the same type, which thereby functions as the unit. In mathematics education literature, this is sometimes referred to as the transition from additive thinking to multiplicative thinking.
ii) In contrast to the situation for whole numbers, we do not have unique names for rational numbers; the number indicated by any given fraction is unchanged if both the numerator and denominator are multiplied by the same factor; and doing computations with fractions often hinges on selecting an appropriate representation, which may involve changing from the representation with which one it initially presented. In particular, to compare or to add or subtract two fractions, it is often necessary to replace the given fractions with equivalent fractions that have the same denominator.1
A fraction is a rational number, which means it can be written as a ratio of a whole number, a relationship between two numbers expressing how many times the first number contains the second number. Common Core defines fractions in two steps;
i) understand a unit fraction 1/b as the quantity formed by 1 part when a whole is partitioned into b equal parts, or equivalently, as a quantity of which it takes b copies to make the whole;
ii) understand a general fraction a/b as the quantity formed by a parts of size 1/b.
A key understanding that will need to be reinforced is that for a fraction, the larger the denominator, the smaller the pieces. There are many models of fractions and I will show them examples using all of the models. Students develop misconceptions about fractions when they think of the numerator and the denominator as separate values; it is difficult for them to see that 2/3 is one number. For this reason, I will give a variety of examples in order for them to create a connection between fractions and other forms of measurement. We call an hour 1/24 of a day because there are 24 hours in one day. Other examples could be a day is 1/7 of a week, since there are 7 days in a week. A cup is 1/4 of a quart since there are 4 cups in a quart.
Set Model
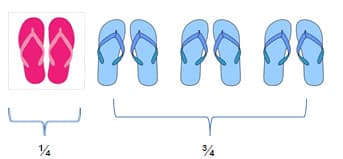
The set model uses a set, meaning a designated piece, to express a fraction. The denominator tells how many total items are contained in the set while the numerator tells how many items are being represented by some qualifier. For example, my set contains 4 pair of flip flops, 1 pair of flip flops are red and the remaining three pair of flip flops are blue. I would then write the fraction 1/4 of the four flip flops are red. I will emphasize that the 1/4 functions as a size comparison. If you were to have four times as many of the red flip flop, you would have as many as are in the whole set of flip flops.
Circular Model
The circular model is a model many third graders see often. Problems usually involve dividing up a pizza into a number of pieces that would represent the denominator. The numerator could be explained as eaten pieces. For example, I brought home a large pizza that was cut into 4 equal pieces. I ate 3 pieces. How much of the pizza was left? The numerator would be the 1 piece left and the denominator would be the total of 4 equal pieces total.

Area Model
The area model has a determined unit, that is most commonly a rectangle due to the ease with which you can partition it evenly and can represent many real-life objects like chocolate bars. The rectangle is partitioned into d equal parts. This rectangle has been partitioned into 4 equal columns and each column shows ¼ unit of the rectangle.
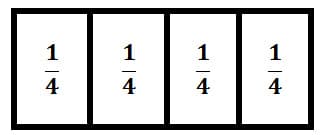
One valuable feature of the rectangle area model is that the unit rectangle can be divided or partitioned into equal pieces, 1/d, of determined size vertically and then further divided or partitioned into another set of equal pieces, 1/b, of determined size horizontally which gives an excellent way to talk about renaming fractions, and will ease students into multiplication of fractions at a later date.
Linear Model
The linear model is represented on a number line, (or more accurately stated a half ray). This model reinforces the notion of length or distance, and most importantly there is a unit of length. The points on the line are labeled by the Measurement Principle.
The Measurement Principle states,
“The number labeling a point tells how far the point is from the origin/endpoint, as a multiple of the unit distance”.2
The end point of the number line is labeled 0 showing that there is 0 distance from this point. The unit interval, (0,1) has a unit length and the point labeled “1” is at distance 1 from 0. The 2 is then placed at the point that is twice a far from 0 as is 1. Therefore, the interval (0,2) is made up of two intervals of unit length, (0,1) and (1,2).

Comments: