Fractions on the Number Line
Once the Measurement Principle has been explained, students should be ready to begin to understand that a fraction is a number and has a place on the number line. In elementary classrooms we technically do not work on a full number line since we only work with positive numbers and only need to go in one direction, positive. We can call this a number ray, a half line with an origin, which we label with a 0, and that travels in one direction from that point. This number ray essentially is just like a ruler. On a ruler, the end point is 0, and the point labeled 1 defines a standard unit of measure, perhaps an inch or a centimeter. Number lines do not need to have a standard unit, and can have an arbitrarily chosen unit to fulfill the desired need.
When students decide on the unit distance, the placement of all other numbers on the ray is determined. The number placed on the ray labels the distance that point is from the endpoint or origin. As I explained above, students should be given an opportunity to explore using rods and measuring items to help them develop an understanding of this principle. This should give them a better grasp as to why the numbers are placed on the number line and can begin to transfer this knowledge to the placement of fractions.
A good place to begin is with the fraction 1/2. A defining property of 1/2 is that 2 of it will make 1. On a number line that has an endpoint defined with 0 and a 1 placed one unit distance from the endpoint, 1/2 will be place so that if you traveled from 0 to 1 you will have traveled that distance two times.
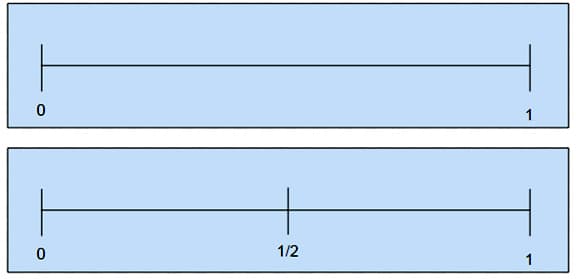
This same principle governs the placement of the other unit fractions. A defining property of 1/3 is that 3 of it make up the unit, so 1/3 should be at a distance from the origin that if you go that distance three times you get to 1.

You can follow the same principle and place 1/4 is that 4 of it make up the unit, so 1/4 should be at a distance from the origin that if you go that distance four times you get to 1.
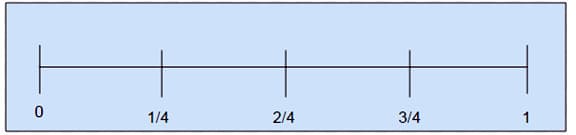
A good teaching sequence using these diagrams would be, show the number line for 1/2., set it up for 1/3, and let students work on it and discuss it, draw it, and then repeat for ¼. If ¼ works fairly quickly, you can ask about 1/5.
It is important to show students number lines that extend past 1. Students will need to see that fractions can be larger than 1. These pictures may help to strengthen the understanding that each unit fraction is indeed a new unit, that provides a finer means of measuring that extends the system of whole numbers.


Comments: